强化学习

强化学习基础

概念

强化学习是一种通过智能体与环境之间的交互来学习如何做出最优决策的机器学习方法。在强化学习中，智能体会根据当前状态做出一个动作，并获得一个反馈信号或奖励，这个奖励可以是正的、负的或零。智能体的目标是在环境中通过试错学习，找到最大化奖励的策略。

强化学习研究的是多序列决策问题，它有有很多应用场景，比如游戏、自动驾驶、机器人控制等。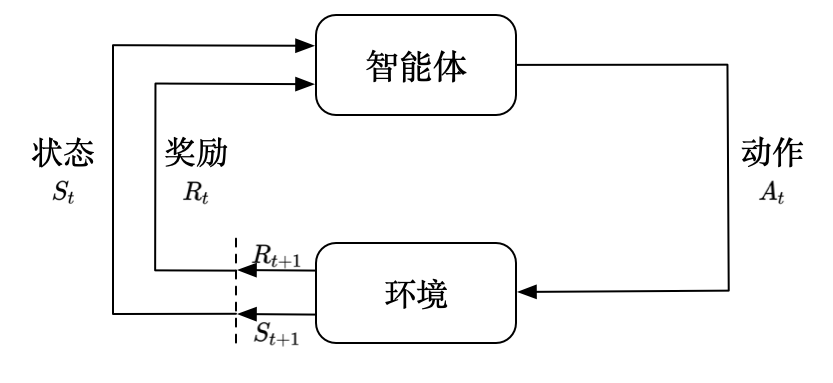

状态满足可重复到达。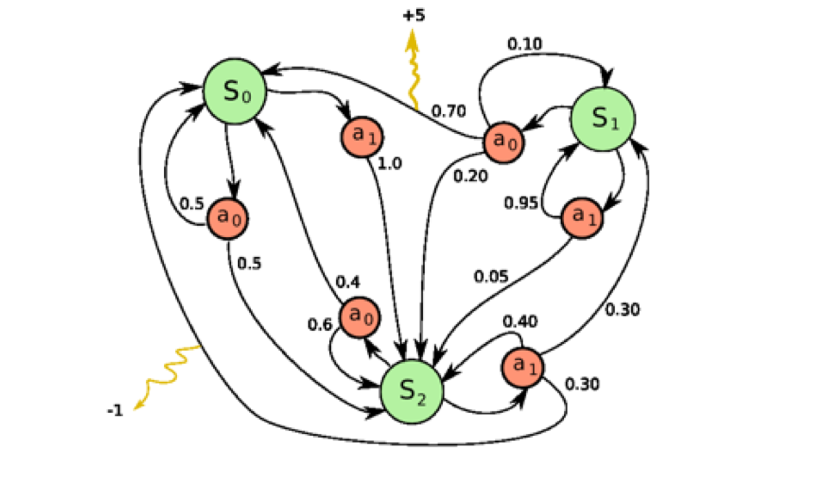

智能体一般包含策略、价值函数和模型中的一个或多个：

• 策略：根据当前状态选取下一步动作，也是最终所需要的
• 价值函数：对当前状态或状态动作对进行评估，是智能体对环境好坏的理解
• 模型：环境的状态转移及奖励函数，智能体对环境处境和变化的理解

策略

策略是智能体的动作模型，它其实是一个函数，决定了智能体的动作。
策略其实就是强化学习最终要得到的东西；之所以需要价值函数、模型这些，是因为强化学习没有直接的监督标签，只有奖励这样的间接的监督信号，所以需要做很多其它工作来更好地得到最佳策略。
策略可以分为两种：

• 随机性策略：就是 $\pi$， 即：$\pi(a|s)=P(a_t=a|s_t=s)$，输入一个状态$s$，输出各个动作的概率，通过采样可以得到具体采用的动作。
• 确定性（deterministic）策略：函数直接输出一个动作，可以看成$a^*=argmax_a\pi(a|s)$

随机性策略具有许多优点，例如：随机性可以更好地探索环境；随机性带来的动作多样性有利于多智能体博弈，防止策略被对手预测。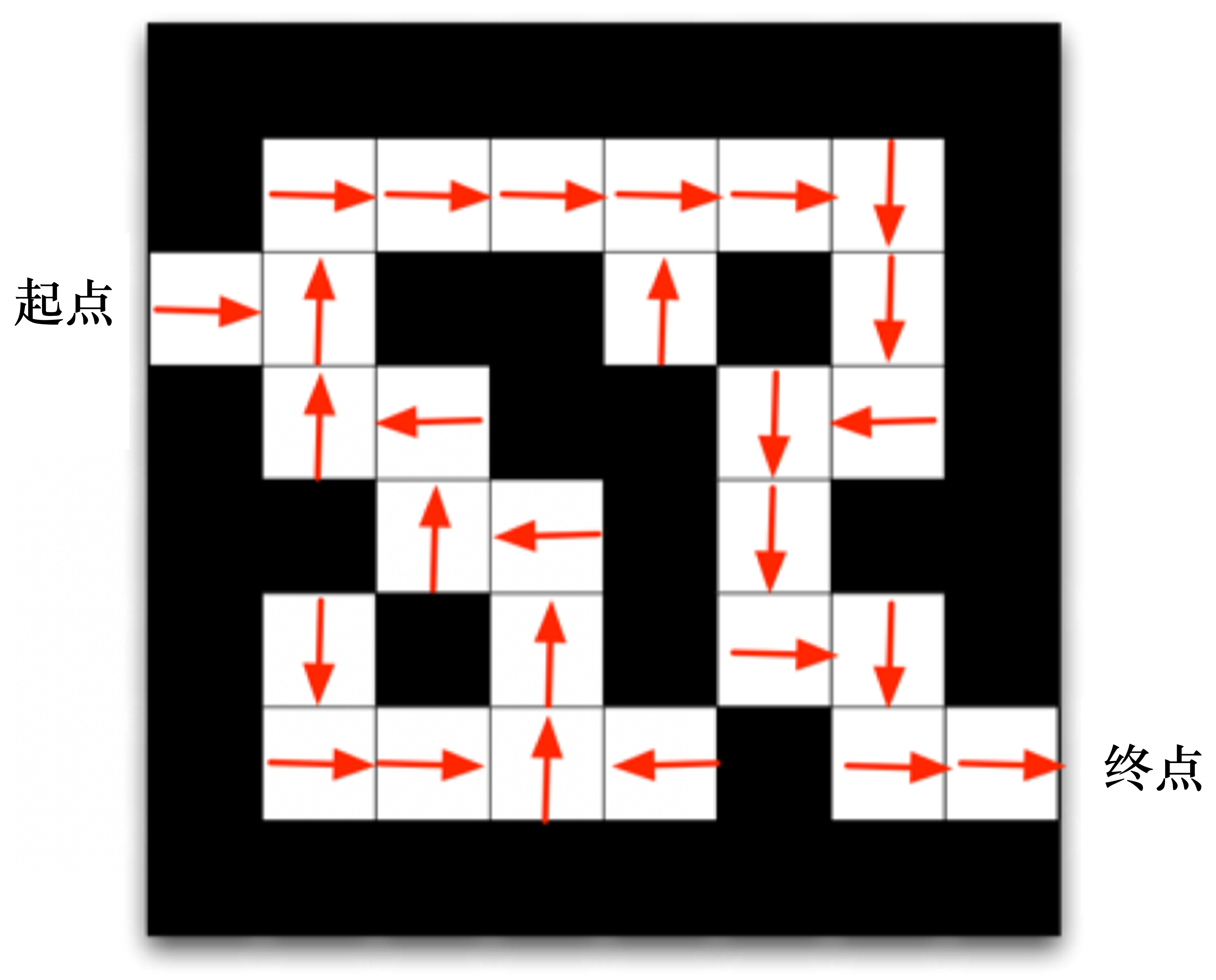

基于策略的走迷宫，每一个状态得到动作

价值函数

价值函数用于评估状态的好坏，反映我们可以得到的奖励的量，其中未来的奖励会通过一个折扣因子$γ$进行加权。
$$V_π(s) = E_π[G_t|s_t=s]=E_π[\sum_{k=0}^∞γ^kr_{t+k+1}|s_t=s]$$
这种价值函数的输入只有状态，另一种价值函数叫Q函数，是将状态和动作共同作为输入：
$$Q_π(s,a) = E_π[G_t|s_t=s,a_t=a]=E_π[\sum_{k=0}^∞γ^kr_{t+k+1}|s_t=s,a_t=a]$$

即可以获得的奖励是由当前状态和采取的动作共同决定的。

基于价值的走迷宫，会得到各个状态（和动作）的价值

模型

模型是对环境进行建模的方式，通过学习环境的动态规律，智能体可以更加有效地规划和执行策略。模型可以是状态转移函数（State Transition Function），表示从一个状态转移到另一个状态的概率：
$$p_{s s^{\prime}}^{a}=p(s_{t+1}=s^{\prime} | s_{t}=s, a_{t}=a)$$
也可以是奖励函数（Reward Function），表示在特定状态下执行某个动作可以获得的奖励：
$$R(s,a)=E[r_{t+1} | s_{t}=s, a_{t}=a]$$

相比之下，价值函数主要用于评估不同策略的优劣，而模型则用于模拟和预测环境的变化。

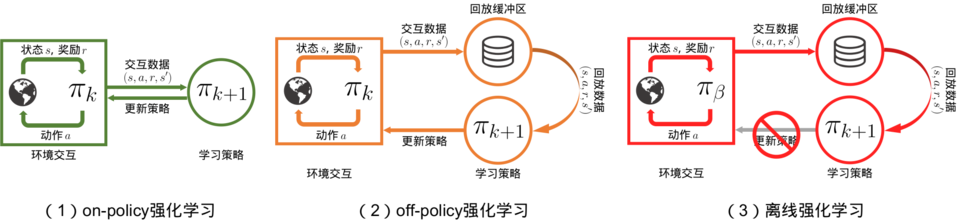
On-policy VS Off-policy

• on-policy(同策略)：策略评估和控制方法使用同一个策略进行训练和测试。也就是说，该策略在采取行动和更新价值函数时都是基于当前策略的，因此不能同时学习多个策略。
• off-policy(异策略)：策略评估和控制方法则可以使用不同的策略进行训练和测试。训练时可以基于一个策略生成样本数据，而评估时则可以基于另一个策略进行测试。这种方法可以更加高效地利用历史数据，同时也允许学习多个策略。

虽然概念如此，但是在实际中，很多算法到底属于On-policy还是Off-policy，不同的人有不同的看法。下面我从贝尔曼方程的角度谈谈我的看法：

• 根据贝尔曼方程：
  $$V(s)=R(s)+\gamma \sum_{s^{\prime} \in S} p(s^{\prime} | s) V(s^{\prime})$$
• 当策略评估和控制方法使用同一个策略时，状态转移关系$\sum_{s^{\prime} \in S} p(s^{\prime} | s)$固定，没有问题；
• 而off-policy中策略评估和控制方法则使用不同的策略，动作概率分布不一致，状态转移关系就会发生变化，会使得下一个状态$s^{\prime}$不一致；
• 进而贝尔曼方程的更新就不严格，也就是说off-policy方法在贝尔曼方程的推导上有问题，也就会带来潜在的模型不收敛。
• 在采用随机性策略时，也可以得到类似推导，即：off-policy在上述贝尔曼方程上的推到是不严谨的。

但是对于使用q值来更新的算法，off-policy则可以规避这个问题：

• 根据q值的贝尔曼方程：
  $$Q(s,a)=R(s,a)+\gamma \sum_{s^{\prime} \in S} p(s^{\prime} | s,a) V(s^{\prime})$$
• 此时即使策略评估和控制方法则使用不同的策略，动作概率分布不一致也没有关系，因为状态转移关系$\sum_{s^{\prime} \in S} p(s^{\prime} | s,a)$中本来就包含了动作，即使动作变了，也没有问题。
• 也就是说更新的$Q(s,a)$就是针对这一动作的更新，而不是针对$V(s)$更新，在这一过程中off-policy方法是严谨的。

有了上面的推论，我们是不是可以认为，严谨的强化学习算法（符合贝尔曼方程）可以通过价值函数（贝尔曼方程）的形式来区分呢。即使用状态价值函数$V(s)$的是on-policy，使用动作价值函数$Q(s,a)$的是off-policy。

从贝尔曼方程的角度来看，Off-policy 更新的状态价值函数与行动策略 $\mu$ 有关，而 On-policy 更新的状态价值函数与当前策略 $\pi$ 相关。因此，Off-policy 更灵活，但可能会产生更大的方差，而 On-policy 更稳定。

def train_on_policy_agent(env, agent, num_episodes):
    return_list = []
    for i in range(10):
        with tqdm(total=int(num_episodes/10), desc='Iteration %d' % i) as pbar:
            for i_episode in range(int(num_episodes/10)):
                episode_return = 0
                transition_dict = {'states': [], 'actions': [], 'next_states': [], 'rewards': [], 'dones': []}
                state = env.reset()
                done = False
                while not done:
                    action = agent.take_action(state)
                    next_state, reward, done, _ = env.step(action)
                    transition_dict['states'].append(state)
                    transition_dict['actions'].append(action)
                    transition_dict['next_states'].append(next_state)
                    transition_dict['rewards'].append(reward)
                    transition_dict['dones'].append(done)
                    state = next_state
                    episode_return += reward
                return_list.append(episode_return)
                agent.update(transition_dict)
                if (i_episode+1) % 10 == 0:
                    pbar.set_postfix({'episode': '%d' % (num_episodes/10 * i + i_episode+1), 'return': '%.3f' % np.mean(return_list[-10:])})
                pbar.update(1)
    return return_list

def train_off_policy_agent(env, agent, num_episodes, replay_buffer, minimal_size, batch_size):
    return_list = []
    for i in range(10):
        with tqdm(total=int(num_episodes/10), desc='Iteration %d' % i) as pbar:
            for i_episode in range(int(num_episodes/10)):
                episode_return = 0
                state = env.reset()
                done = False
                while not done:
                    action = agent.take_action(state)
                    next_state, reward, done, _ = env.step(action)
                    replay_buffer.add(state, action, reward, next_state, done)
                    state = next_state
                    episode_return += reward
                    if replay_buffer.size() > minimal_size:
                        b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
                        transition_dict = {'states': b_s, 'actions': b_a, 'next_states': b_ns, 'rewards': b_r, 'dones': b_d}
                        agent.update(transition_dict)
                return_list.append(episode_return)
                if (i_episode+1) % 10 == 0:
                    pbar.set_postfix({'episode': '%d' % (num_episodes/10 * i + i_episode+1), 'return': '%.3f' % np.mean(return_list[-10:])})
                pbar.update(1)
    return return_list

与监督学习的区别

• 监督学习的数据是独立同分布的，而强化学习是存在前后关联的序列数据
• 强化学习的奖励是延迟的

智能体类型

基于策略（policy-based）

直接学习策略，输入环境状态，输出对应动作（的概率）。

常见算法：Policy Gradient

基于价值（value-based）

直接学习价值函数，隐式学习策略。通过价值函数可以推算策略。

基于价值的方法需要维护一个价值表格或价值函数，并通过价值表格或价值函数来选取价值最大的动作，这种迭代只能运用在离散的环境下，不适合动作集合庞大、动作连续的场景。
基于价值相比基于策略训练起来效果更好，更平稳，因为只要训练好Q函数，就可以保证策略是最好的，而训练Q函数是一个单纯的回归问题。
常见算法：Q-learning，Sarsa

演员-评论员（actor-critic）

既学习策略，又学习价值函数。

根据策略做出动作，同时根据价值函数给出的价值来加速学习过程。

基于模型

通过建立模型学习状态转移来采取行动。

免模型方法一般采用数据驱动方法，当学习过程较为困难且有一定先验知识时，可以通过建立模型来降低难度，提升泛化效果，缓解数据稀疏等问题。

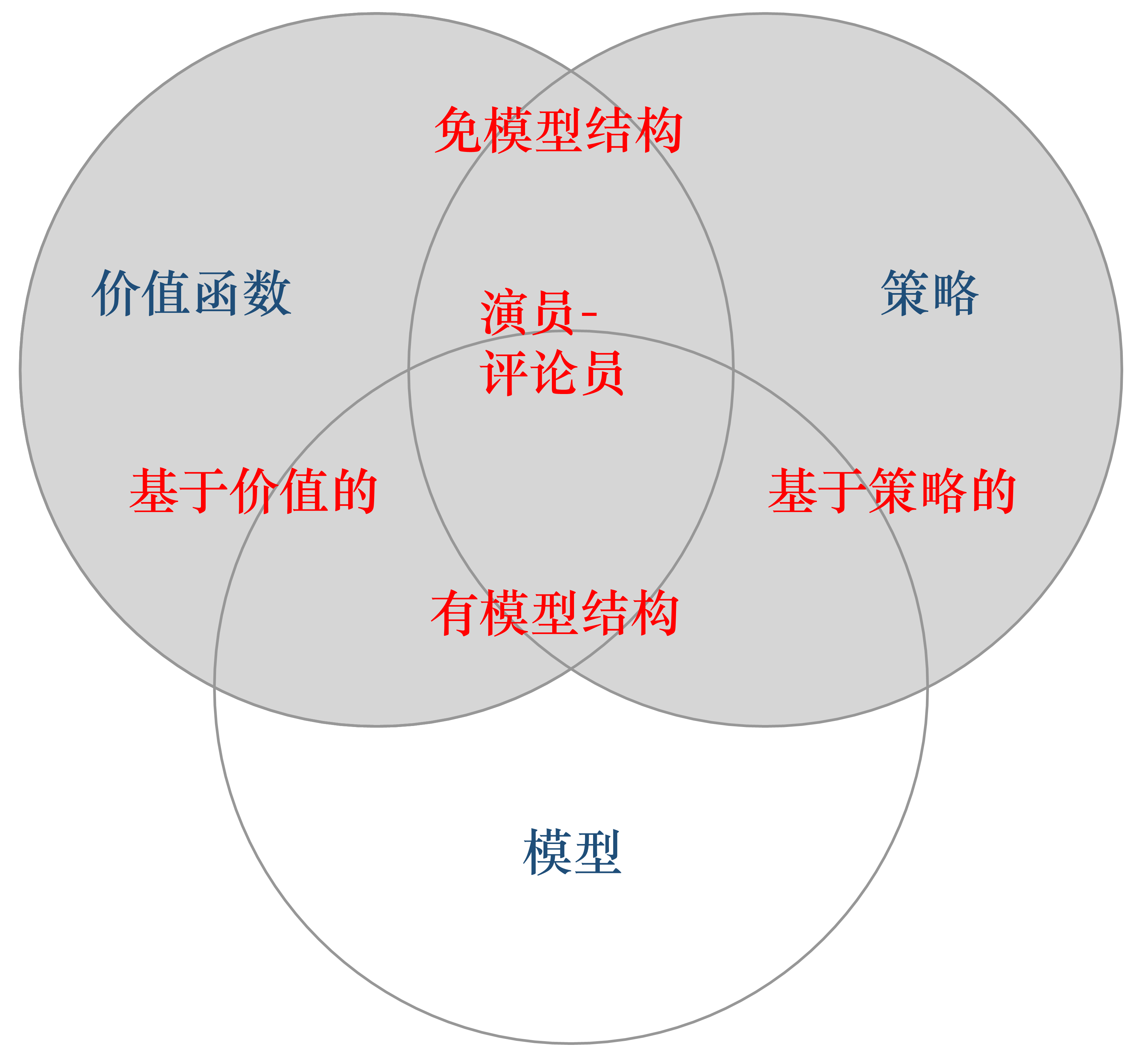
算法类型

不同算法有不同的适用场景：

动作空间	算法
离散	Sarsa、Q-learning、DQN
连续	DDPG、TD3
both	PG、AC、A2C、TRPO、PPO、SAC

• On-policy vs Off-policy

优化策略	算法
在线	Sarsa、PG、AC、A2C、TRPO、PPO
离线	Q-learning、DQN、DDPG、TD3

• 注：
  • 此处的依据是是否更新Q值，是否可以严谨地使用历史数据；
  • Sarsa貌似是在更新Q值，但是Sarsa的公式并不是严格的动作价值函数贝尔曼方程，也就不算off-policy，当然文献中怎么叫的都有。
  • PPO虽然可以用历史数据，但是它使用的不是动作价值函数，并不能严格使用历史数据，为了避免不收敛使用clip等方式限制不严格的程度。

策略	算法
随机性	PG、AC、A2C、TRPO、PPO
确定性	DDPG

探索&利用

概念

• 探索：尝试不同的动作来得到最佳策略，不一定能获得最优收益
• 利用：采用已知可以得到很大奖励的动作
• 学习：在未知的环境中，通过学习与环境交互来改进策略
• 规划：基于当前状态规划并寻找最优动作

探索方式

• 添加噪声：$\epsilon-greedy$
• 积极初始化（optimistic initialization）：给各个动作一个较高的初始期待，增加智能体探索未使用动作的概率。
• 基于不确定性的度量：尝试具有不确定收益的策略，可能带来更高的收益
  • 上置信界法UCB：探索少的动作，不确定性高，可能的潜在收益高，可以将这个分数加到价值函数上。
  • 汤普森采样
• 概率匹配：随机性策略，根据概率采样

强化学习实验

gym

gym是由openAI开源的一个强化学习库，里面包含了很多的环境（游戏）

常见用法

import gym
env = gym.make('环境名') # 构建实验环境
observation = env.reset() # 重置并获得初始状态
for step in range(100):
    env.render()   # 显示图形界面
    action = agent(observation)
    observation, reward, done, info = env.step(action)   # 提交动作并返回观察、奖励等信息
env.close() # 关闭环境

stable_baselines3

常见用法

import gym
from stable_baselines3 import PPO
from stable_baselines3.common.env_util import make_atari_env,make_vec_env
from stable_baselines3.common.atari_wrappers import AtariWrapper

env = gym.make("ALE/BattleZone-ram-v5")
# env = AtariWrapper("ALE/BattleZone-v5")
# env = make_vec_env(env, n_envs=20)
# env = make_atari_env("ALE/BattleZone-ram-v5", n_envs=20)

model = PPO("MlpPolicy", env, verbose=1)
# model.set_parameters("ppo_ALE/BattleZone-v5-1")
model.learn(total_timesteps=2000000, log_interval=40)
model.save("ppo_ALE/BattleZone-ram-v5-1")

obs = env.reset()
while True:
    action, _states = model.predict(obs, deterministic=True)
    obs, reward, done, info = env.step(action)
    env.render()
    time.sleep(0.1)
    if done:
        break

RAY&rllib

RAY

以非常简洁的方式实现多进程、进程间通信、资源控制等
多进程：


只需要通过装饰器对普通函数进行修饰，并在调用时加入remote，就可以新开后台进程执行

tune

基于RAY的调参工具，自动化，简洁

RLLib

基于RAY和tune实现强化学习

马尔科夫决策过程

智能体与环境交互，观察环境状态、采取动作改变环境，然后得到奖励并进一步观察环境状态的过程可以通过马尔科夫决策过程（MDP）来表示

马尔科夫过程（MP）

马尔科夫性质

随机过程中，在给定过去和现在状态的情况下，随机变量未来状态的条件概率分布仅依赖当前状态。
核心是：只取决于现在，而与过去独立：
$$p(X_{t+1}=x_{t+1} |X_{0:t}=x_{0: t})=p(X_{t+1}=x_{t+1} |X_{t}=x_{t}) $$

如果过程不满足马尔科夫性质，可以使用循环神经网络、注意力机制等

马尔科夫链

一组随机变量序列，满足马尔科夫性质，则称为马尔科夫过程。
离散时间的马尔科夫过程称为马尔科夫链：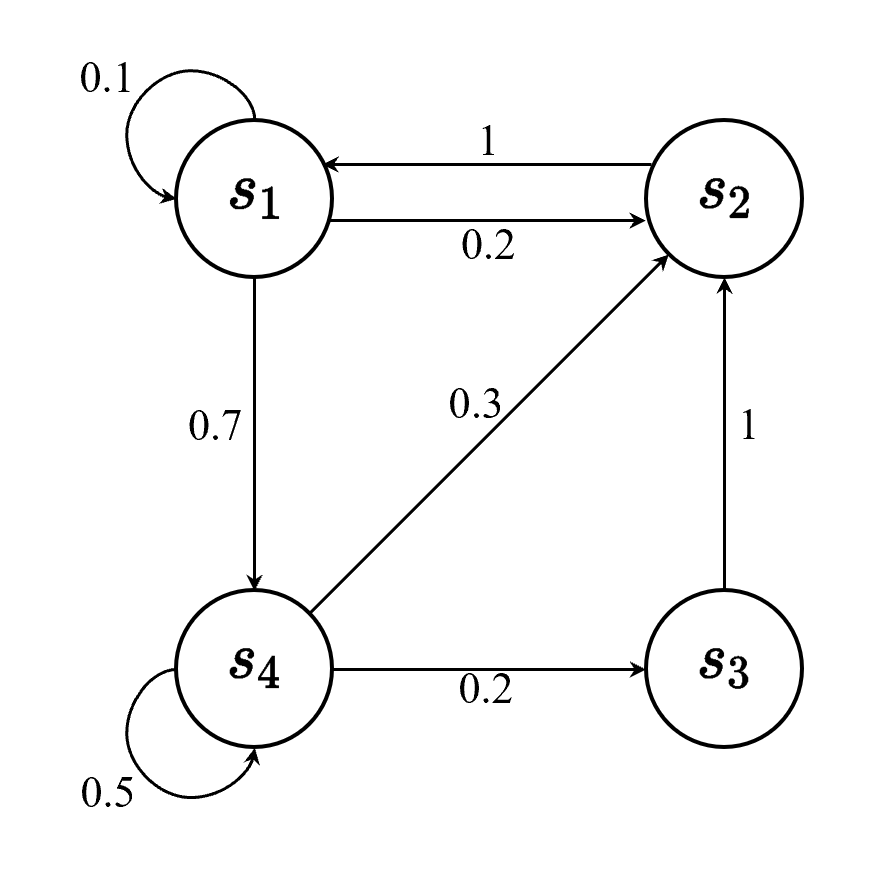

因为每个状态转移只取决于一个状态，所以马尔科夫链的转移过程可以用状态转移矩阵来表示。

马尔科夫奖励过程

• 马尔科夫奖励过程是在马尔科夫链的基础上增加了奖励函数R。
• 奖励函数表示当达到某一个状态的时候可以获得多大的奖励。
• 当状态数有限的时候，R可以是一个向量。

回报与价值函数

范围：一个回合的长度
回报：奖励的逐步叠加
$$G_{t}=r_{t+1}+\gamma r_{t+2}+\gamma^{2} r_{t+3}+\gamma^{3} r_{t+4}+\ldots+\gamma^{T-t-1} r_{T}$$
状态价值函数：回报的期望
$$ V^{t}(s) =E[G_{t} | s_{t}=s]
=E[r_{t+1}+\gamma r_{t+2}+\gamma^{2} r_{t+3}+\ldots+\gamma^{T-t-1} r_{T} | s_{t}=s] $$

贝尔曼方程

$$
V(s)=R(s)+\gamma \sum_{s^{\prime} \in S} p(s^{\prime} | s) V(s^{\prime})
$$
通过贝尔曼方程，可以将当下状态的价值表示成当下状态的奖励和转移状态的价值组成。
转移状态的价值需要加上一个折扣系数和转移概率。

迭代计算马尔科夫奖励过程的价值

蒙特卡洛法

产生大量的轨迹，计算回报的均值

动态规划

对于所有状态，不断通过贝尔曼方程进行更新迭代，直至状态的价值收敛

马尔科夫决策过程

在马尔科夫奖励过程的基础上增加了决策（动作）
在状态转移方面增加了一个条件，变成了：
$$
p(s_{t+1}=s^{\prime} | s_{t}=s,a_{t}=a)
$$
不仅取决于状态，还取决于动作。
同时奖励函数也多了一个形式：
$$
R(s_{t}=s, a_{t}=a)=E[r_{t} | s_{t}=s, a_{t}=a]
$$
即动作和状态共同影响可能得到的奖励

策略

动作由策略基于状态得到：
$$
\pi(a |s)=p(a_{t}=a | s_{t}=s)
$$
当策略确定的时候，每个状态会采取的动作概率一定，此时马尔科夫决策过程可以退化为马尔科夫奖励过程：
$$
P_{\pi}(s^{\prime} | s)=\sum_{a \in A} \pi(a | s) p(s^{\prime} | s, a)
$$
$$
r_{\pi}(s)=\sum_{a \in A} \pi(a | s) R(s, a)
$$

区别

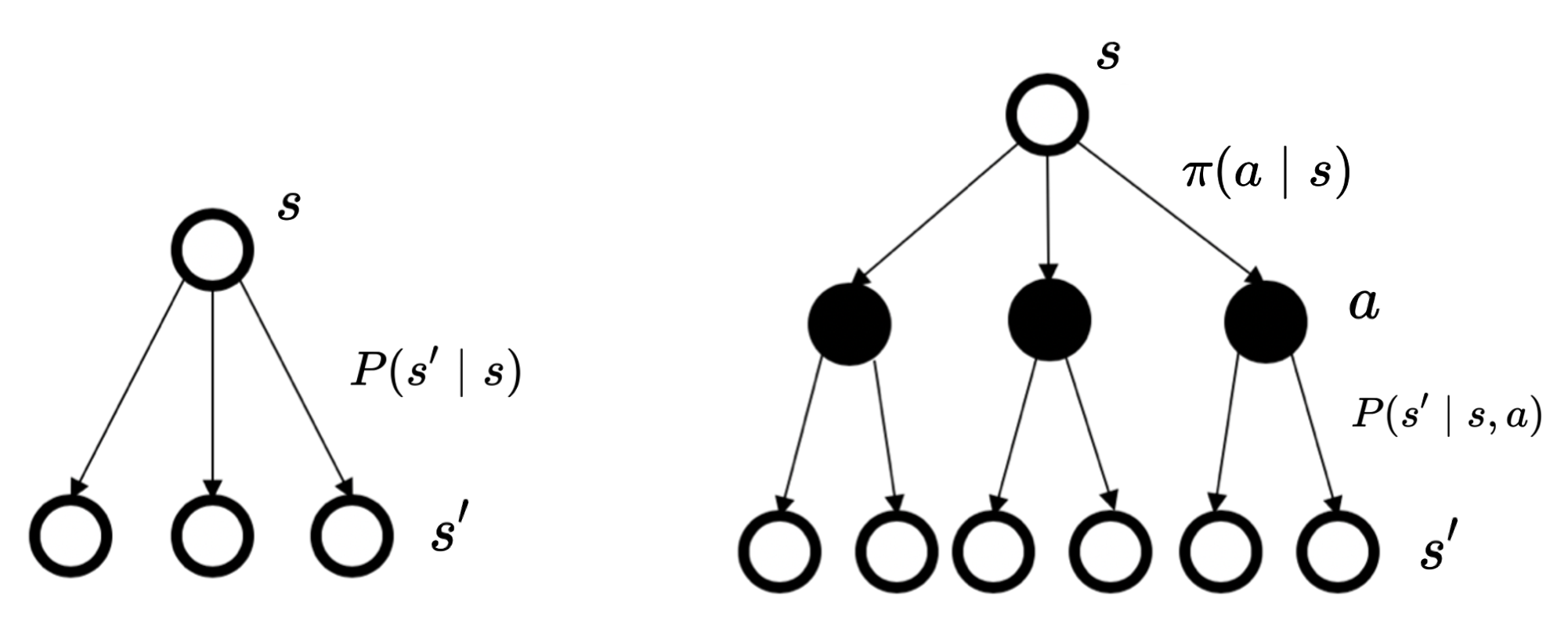马尔科夫过程和马尔科夫奖励过程可以看成是一种静态的情况，概率转移、奖励、价值都是固定的。 而马尔科夫决策过程增加了决策环节，智能体通过动作影响了状态的概率转移，进而影响了状态的价值。因此马尔科夫决策过程具有动态的特性，智能体可以改变环境，争取奖励最大化。

Q函数

马尔科夫决策过程中的价值函数需要考虑动作，即动作价值函数，又称Q函数：
$$
Q_{\pi}(s, a)=E_{\pi}[G_{t} |s_{t}=s, a_{t}=a]
$$
通过对Q函数中的动作进行加权，可以得到价值函数：
$$
V_{\pi}(s)=\sum_{a \in A} \pi(a | s) Q_\pi(s, a)
$$
贝尔曼方程：
$$
Q(s,a)=R(s,a)+\gamma \sum_{s^{\prime} \in S} p(s^{\prime} | s,a) V(s^{\prime})
$$

最佳策略搜索

就是找到一个最大的价值函数，使得：
$$
\pi^{*}(s)=\underset{\pi}{\arg \max } ~ V_{\pi}(s)
$$
常用策略有策略迭代和价值迭代

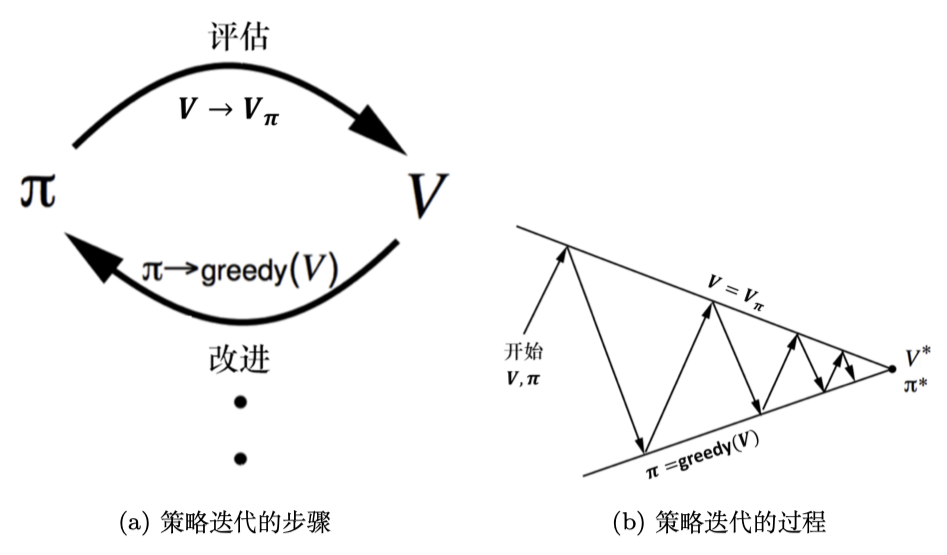
策略迭代

1. 根据策略计算价值函数和Q函数；
2. 最大化Q函数来优化策略。

$$ Q_{\pi_{i}}(s, a)=R(s, a)+\gamma \sum_{s^{\prime} \in S} p(s^{\prime} \mid s, a) V_{\pi_{i}}(s^{\prime}) $$ $$ \pi_{i+1}(s)=\underset{a}{\arg \max } ~Q_{\pi_{i}}(s, a) $$

Q学习迭代：

$$
Q^*(s, a)=R(s, a)+\gamma \sum_{s^{\prime} \in S} p(s^{\prime} | s, a) \max_{a^{\prime}} Q^*(s^{\prime}, a^{\prime})
$$

价值迭代

1. 初始化价值；
2. 根据价值计算Q函数；
3. 最大化Q函数来得到价值
   $$
   Q_{k+1}(s, a)=R(s, a)+\gamma \sum_{s^{\prime} \in S} p(s^{\prime} | s, a) V_{k}(s^{\prime})
   $$
   $$
   V_{k+1}(s)=\max_{a} Q_{k+1}(s, a)
   $$

策略迭代是在价值函数收敛后更新策略，而价值迭代在每一次价值函数更新后都进行策略提升，效率更高。

占用度量

在一个环境中，某个状态被访问的频率。具体来说，占用度量表示在训练过程中代理在不同时间访问每个状态的频率。

占用度量可以被用来评估代理的行为和性能，以及确定哪些状态是最重要的。占用度量还可以被用来计算不同策略的收益，从而帮助代理选择最优策略。

基于价值

表格型方法

通过一个表格记录每一种状态下采取一种动作可以得到的奖励，奖励包括直接奖励和折扣的未来奖励。
常见的表格型方法包括：蒙特卡洛、Q学习、Sarsa
其中蒙特卡罗法是按回合更新，而Q学习、Sarsa是按单步更新

差分时序

强化：可以通过下一个状态的价值来更新当前状态的价值。这种单步更新的方法又称时序差分法。
时序差分目标：
$$
r_{t+1}+\gamma V(s_{t+1})
$$
时序差分误差：
$$
\delta=r_{t+1}+\gamma V(s_{t+1})-V(s_{t})
$$
时序差分法：
$$
V(s_{t}) \leftarrow V(s_{t})+\alpha(r_{t+1}+\gamma V(s_{t+1})-V(s_{t}))
$$

把时序差分方法进行进一步的推广，之前是只往前走一步，即TD(1)。
可以调整步数（step），变成n步时序差分（n-step TD）。比如TD(2)，即往前走两步，利用两步得到的回报，使用自举来更新状态的价值。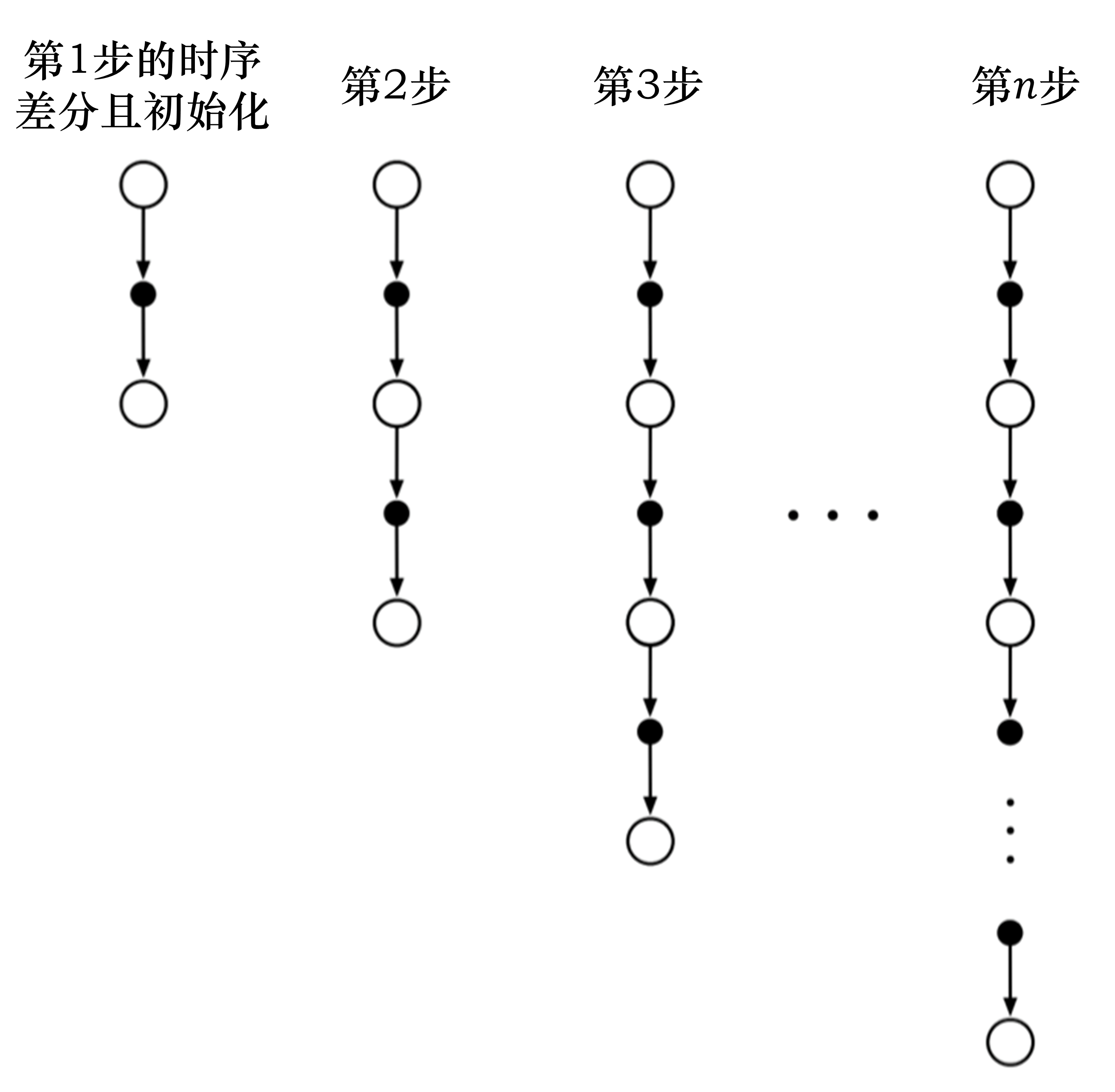

$$
n=1 \qquad G_{t}^{(1)}=r_{t+1}+\gamma V(s_{t+1})\\
n=2 \qquad G_{t}^{(2)}= r_{t+1}+\gamma r_{t+2}+\gamma^{2} V(s_{t+2}) \\
\vdots \\
n=\infty \qquad G_{t}^{\infty}=r_{t+1}+\gamma r_{t+2}+\ldots+\gamma^{T-t-1} r_{T}
$$
如果时序差分方法需要更广度的更新，就变成了 动态规划方法（因为动态规划方法是把所有状态都考虑进去来进行更新）。
如果时序差分方法需要更深度的更新，就变成了蒙特卡洛方法。
图右下角是穷举搜索的方法（exhaustive search），穷举搜索的方法不仅需要很深度的信息，还需要很广度的信息。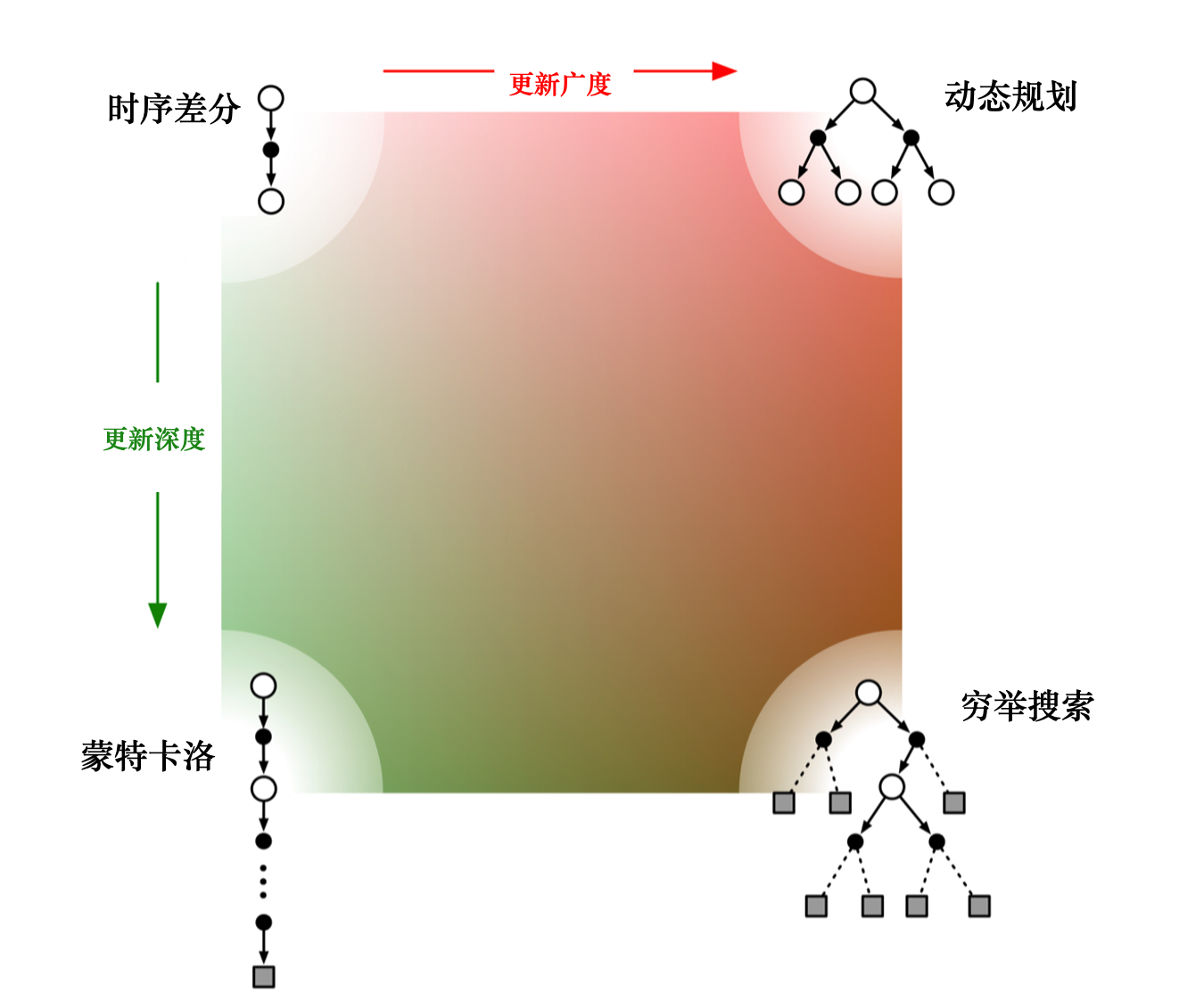

Sarsa

将差分时序中的价值函数改为了Q函数：
$$
Q(s_{t}, a_{t}) \leftarrow Q(s_{t}, a_{t})+\alpha[r_{t+1}+\gamma Q(s_{t+1}, a_{t+1})-Q(s_{t}, a_{t})]
$$

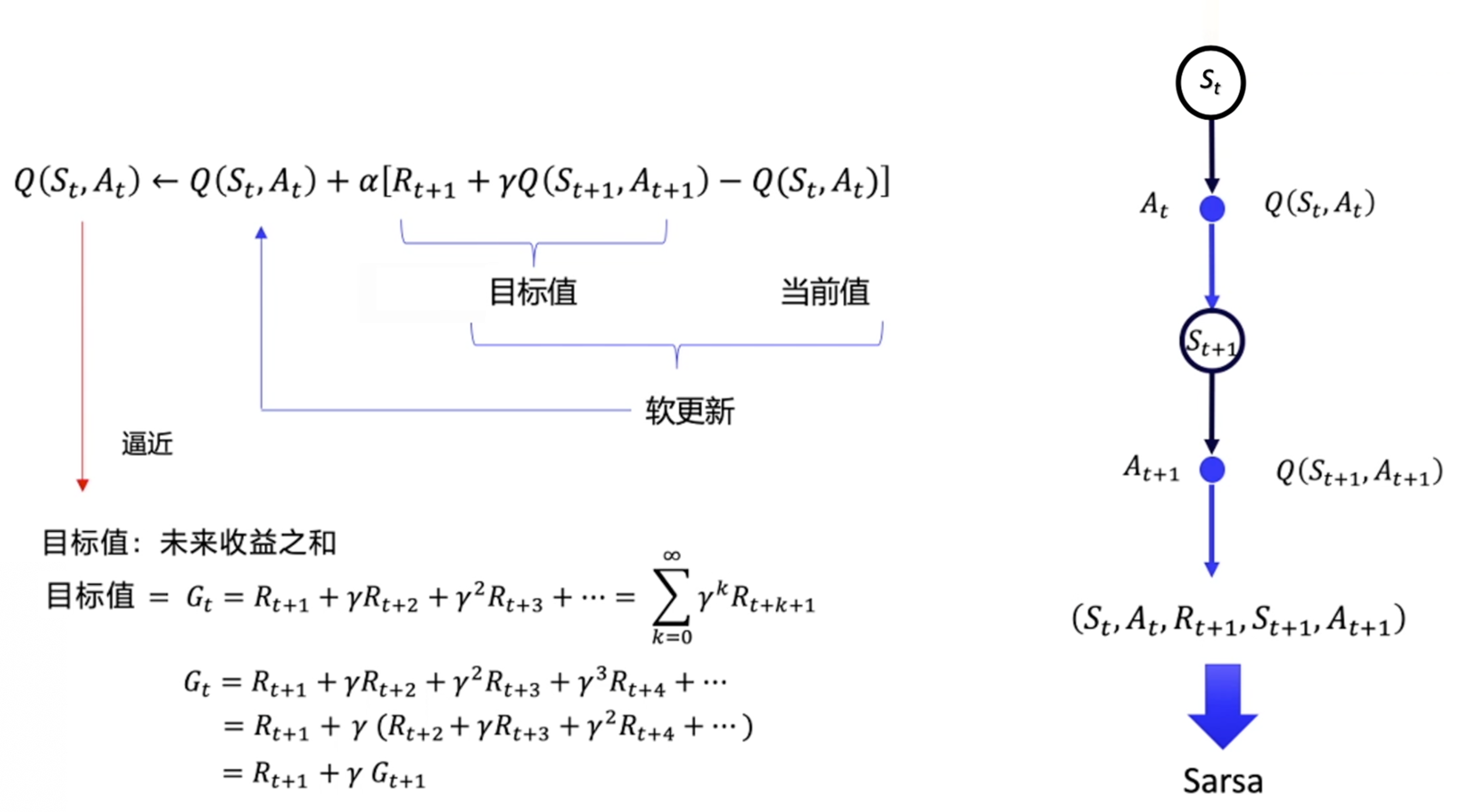
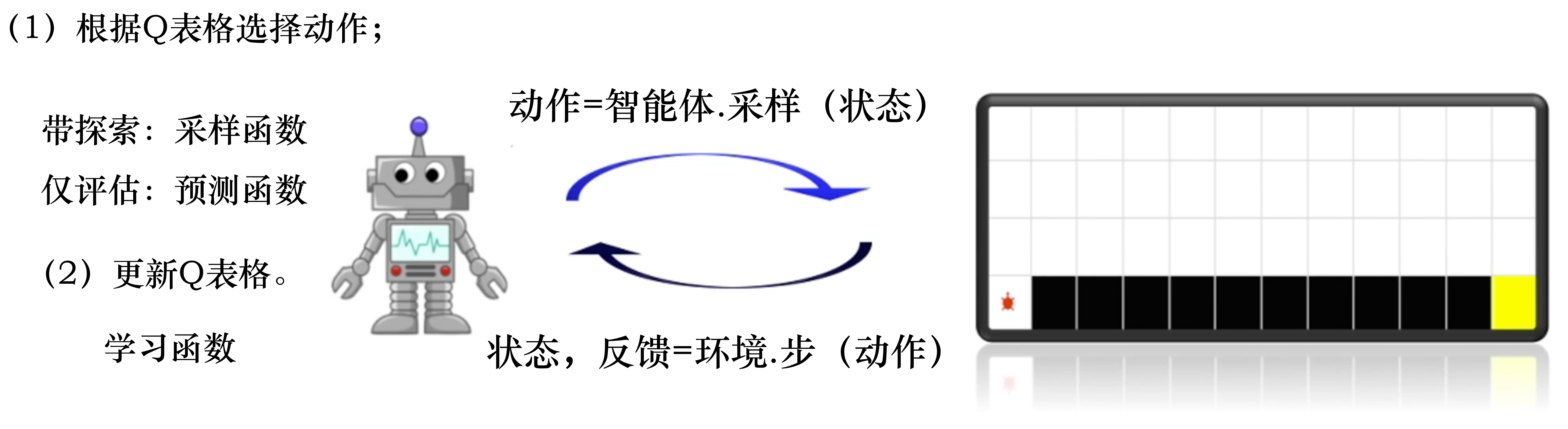
流程：

1. 根据Q表格选择并输出动作；
2. 获取Sarsa五元组，更新Q表格。

但是在Q表格更新后，$V(s_{t+1})$不一定等于$Q(s_{t+1}, a_{t+1})$；
所以Sarsa不能在off-policy场景下使用历史数据，只能在on-policy下用当下数据

Q学习

将Sarsa的时序差分目标改为了$r_{t+1}+\gamma\max_a Q(s_{t+1}, a)$：
$$
Q(s_{t}, a_{t}) \leftarrow Q(s_{t}, a_{t})+\alpha[r_{t+1}+\gamma\max_a Q(s_{t+1}, a)-Q(s_{t}, a_{t})]
$$
这种调整使得Q学习可以使用历史数据。
Q学习是off-policy的时序差分学习方法，Sarsa是on-policy的时序差分学习方法。 Sarsa在更新 Q 表格的时候，它用到的是 $A’$ 。我们要获取下一个 Q 值的时候，$A’$是下一个步骤一定会执行的动作，这个动作有可能是$\varepsilon$-贪心方法采样出来的动作，也有可能是最大化 Q 值对应的动作，也有可能是随机动作，但这是它实际执行的动作。 但是 Q学习在更新 Q 表格的时候，它用到的是 Q 值 $Q(S’,a)$ 对应的动作 ，它不一定是下一个步骤会执行的实际的动作，因为我们下一个实际会执行的那个动作可能会探索。 Q学习默认的下一个动作不是通过行为策略来选取的，Q学习直接看Q表格，取它的最大化的值，它是默认 $A’$ 为最佳策略选取的动作，所以 Q学习在学习的时候，不需要传入 $A’$，即 $a_{t+1}$ 的值。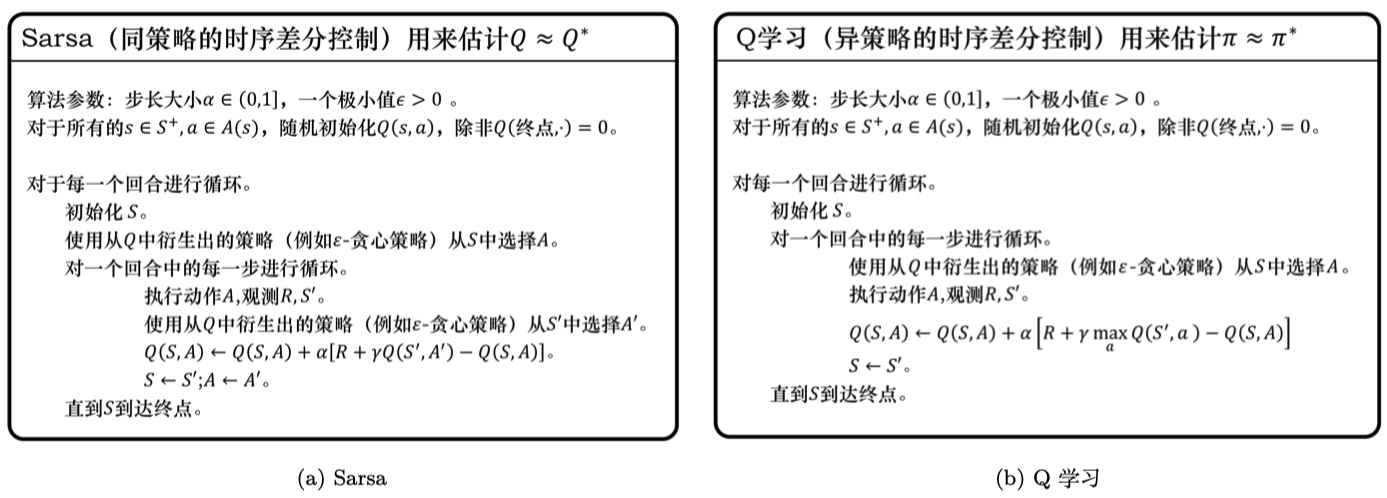

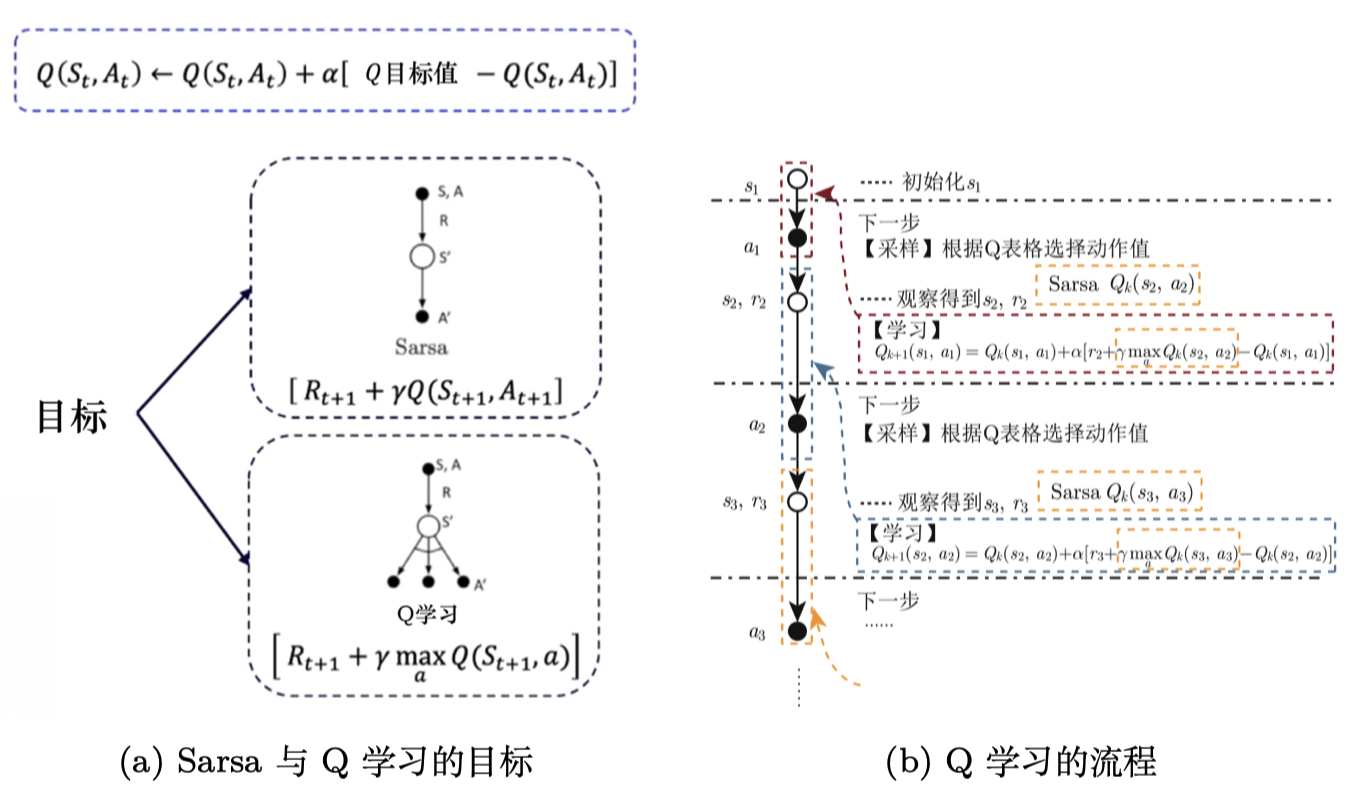
一般来说，Q学习使用选取最大值的最大化操作，估计的Q值偏大，因此更加激进一些；
而Sarsa估计的Q值可能偏小，则较为保守。

DQN

概念

价值函数近似

传统的强化学习通过表格来记录价值函数或动作价值函数，这样有局限：

• 状态空间或动作空间较大时无法存储；
• 状态空间或动作空间为连续值时无法存储；
• 泛化能力不足。

可以通过Q网络进行价值函数近似：
$$
Q_{\phi}(\boldsymbol{s}, \boldsymbol{a}) \approx Q_{\pi}(\boldsymbol{s}, \boldsymbol{a})
$$
其中$Q_{\phi}(\boldsymbol{s}, \boldsymbol{a})$是一个参数为$\phi$的函数，比如神经网络，其输出为一个实数。

深度Q网络（deep Q-network，DQN）是指基于深度学习的Q学习算法，主要结合了价值函数近似与神经网络技术，并采用目标网络和经历回放的方法进行网络的训练。

状态价值函数

状态价值函数输入状态，得到这个状态的价值。 有两种方法：蒙特卡罗法和时序差分法

蒙特卡罗法

蒙特卡罗法在一个回合的游戏结束后才能知道每个状态的价值，并更新网络。 一方面比较慢；另一方面方差较大，因为累计奖励是很多奖励的和，每一个状态都具有随机性。

时序差分法

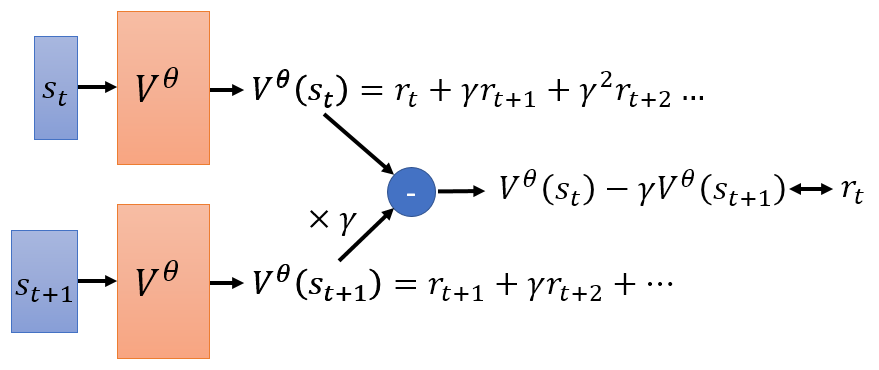时序差分法在每一步就可以更新，让两个状态的差等于所获得的奖励，速度更快，且方差更小

动作价值函数

与状态价值函数类似的还有动作价值函数（Q函数），动作价值函数的输入是一个状态-动作对，其指在某一个状态采取某一个动作，假设我们都使用策略π，得到的累积奖励的期望值有多大。
Q函数有一个需要注意的问题是，策略$ \pi$在看到状态s的时候，它采取的动作不一定是a。Q函数假设在状态s强制采取动作a，而不管我们现在考虑的策略$ \pi$会不会采取动作a，这并不重要。在状态s强制采取动作a。接下来都用策略$ \pi$继续玩下去，就只有在状态s，我们才强制一定要采取动作a，接下来就进入自动模式，让策略$ \pi$继续玩下去，得到的期望奖励才是$ Q_{\pi}(s,a)$。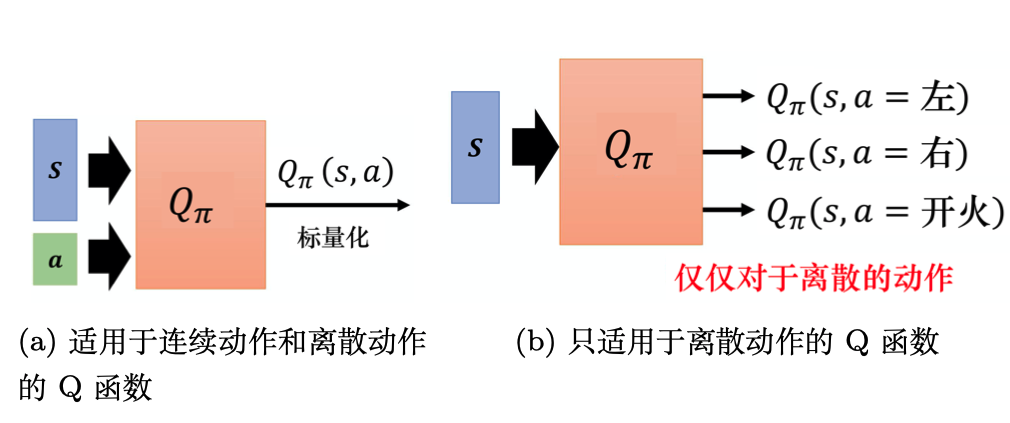

Q函数有两种写法：

1. 输入是状态与动作，输出就是一个标量。这种Q函数既适用于连续动作（动作是无法穷举的），又适用于离散动作。
2. 输入是一个状态，输出就是多个动作值。这种Q函数只适用于离散动作。

在使用Q函数进行策略改进的过程是根据策略调整Q函数，然后根据Q函数更新策略，且新策略一定比以前的策略更好。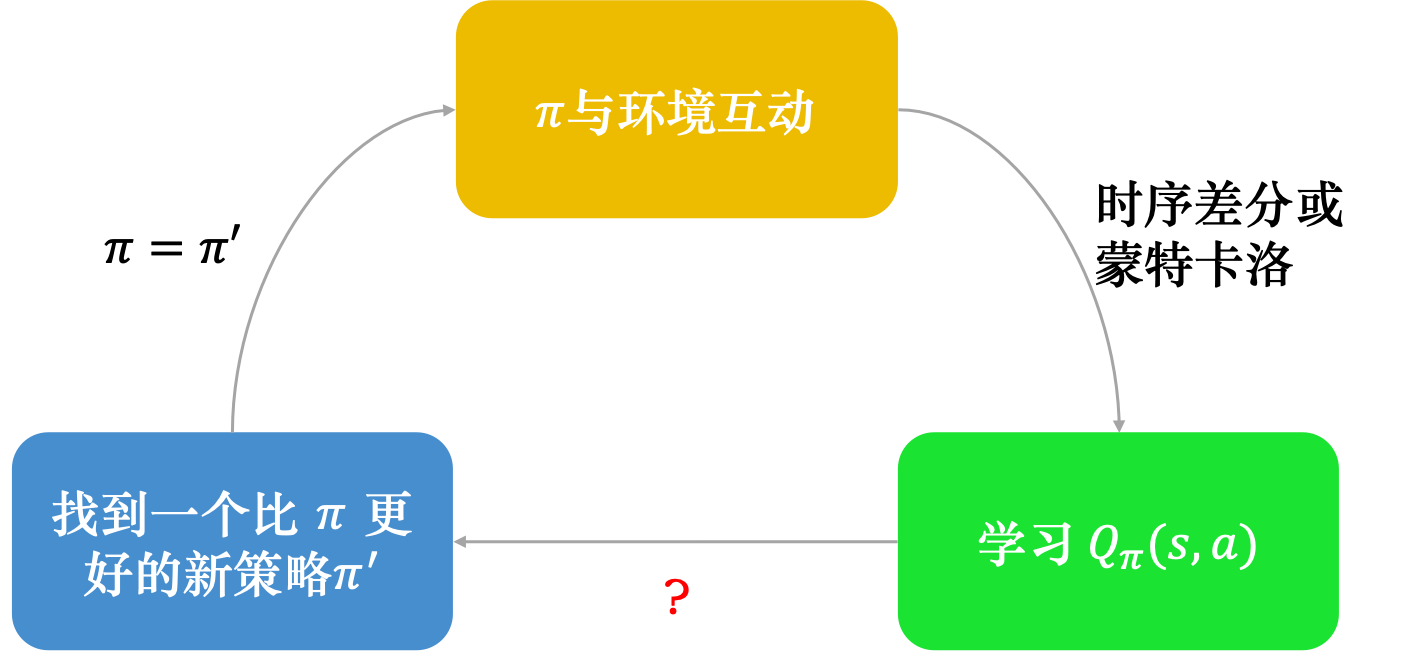

$$
\pi^{\prime}(s)=\underset{a}{\arg \max} Q_{\pi}(s, a)
$$

目标网络

通过时序差分法训练Q函数的时候的拟合目标为：
$$
Q_{\pi}(s_{t}, a_{t}) =r_{t}+\gamma Q_{\pi}(s_{t+1}, \pi(s_{t+1}))
$$
此时右边的目标是变动的，会导致训练过程不稳定。
目标网络的做法是先把右边冻住，只更新左边的网络，在更新一定轮次后用左边的新参数覆盖右边网络的参数。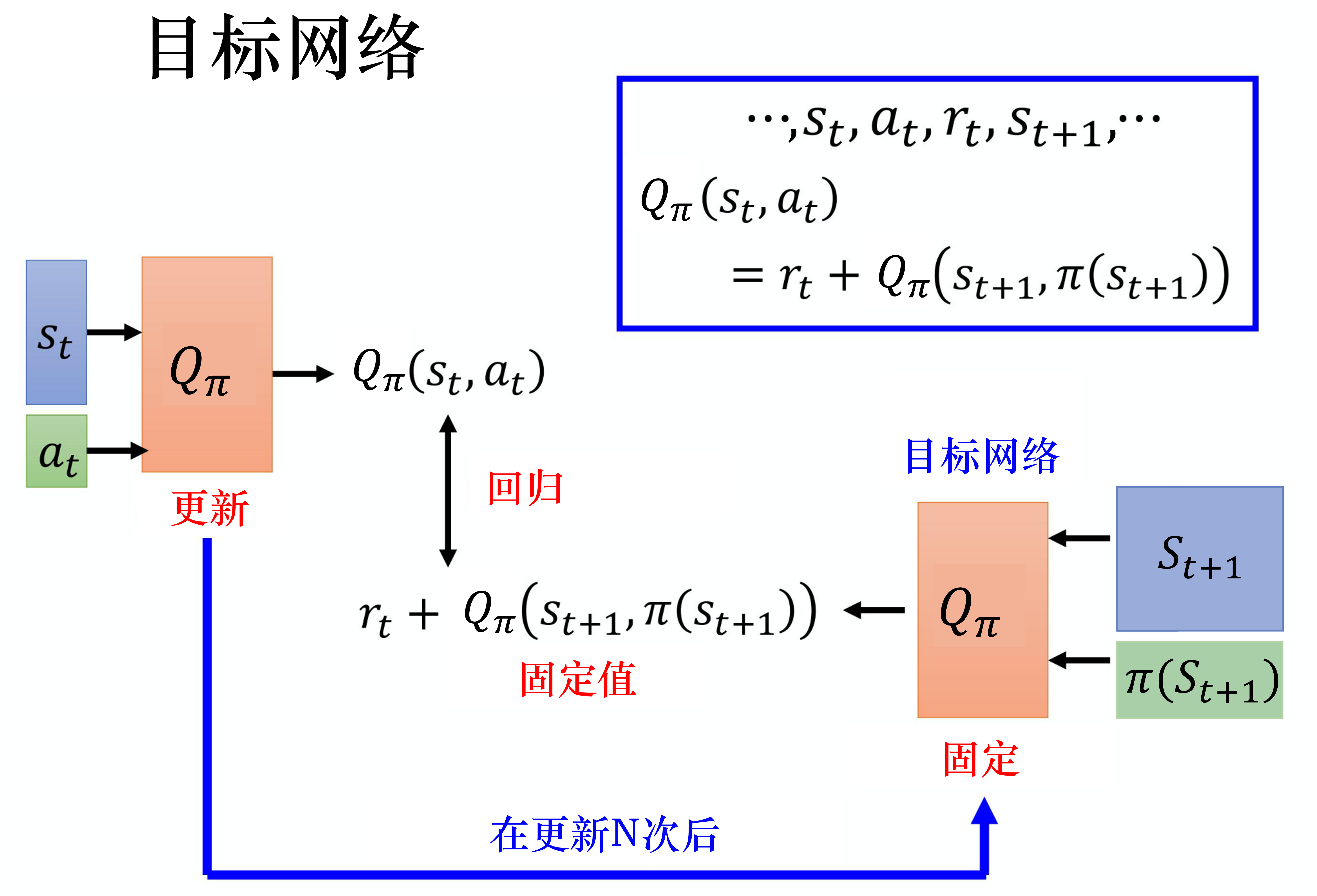

探索

因为强化学习会加强有收益的动作，所以如果一个动作产生了收益，就会加强，使得其它没有出现的动作更不可能出现。
一种方法是在一定概率下采取随机动作，这个概率在训练初期较大，在训练后期较小：
$$
a= \begin{cases} \underset{a}{\arg \max} Q(s, a) & \text {, 有 } 1-\varepsilon \text { 的概率 } \\ \text { 随机} & \text {, 否则 } \end{cases}
$$
另一种方式是玻尔兹曼探索：
$$
\pi(a \mid s)=\frac{\mathrm{e}^{Q(s, a) / T}}{\sum_{a^{\prime} \in A} \mathrm{e}^{Q(s, a^{\prime}) / T}}
$$
一方面将取max动作改为了按概率采样；另一方面通过温度系数T调整分布的平缓程度，以给小概率事件更大或更小的采样概率。

经验回放

• 在强化学习中，跟环境交互获得数据是比较耗时的；
• 数据非常相似，缺乏多样性不利于训练。 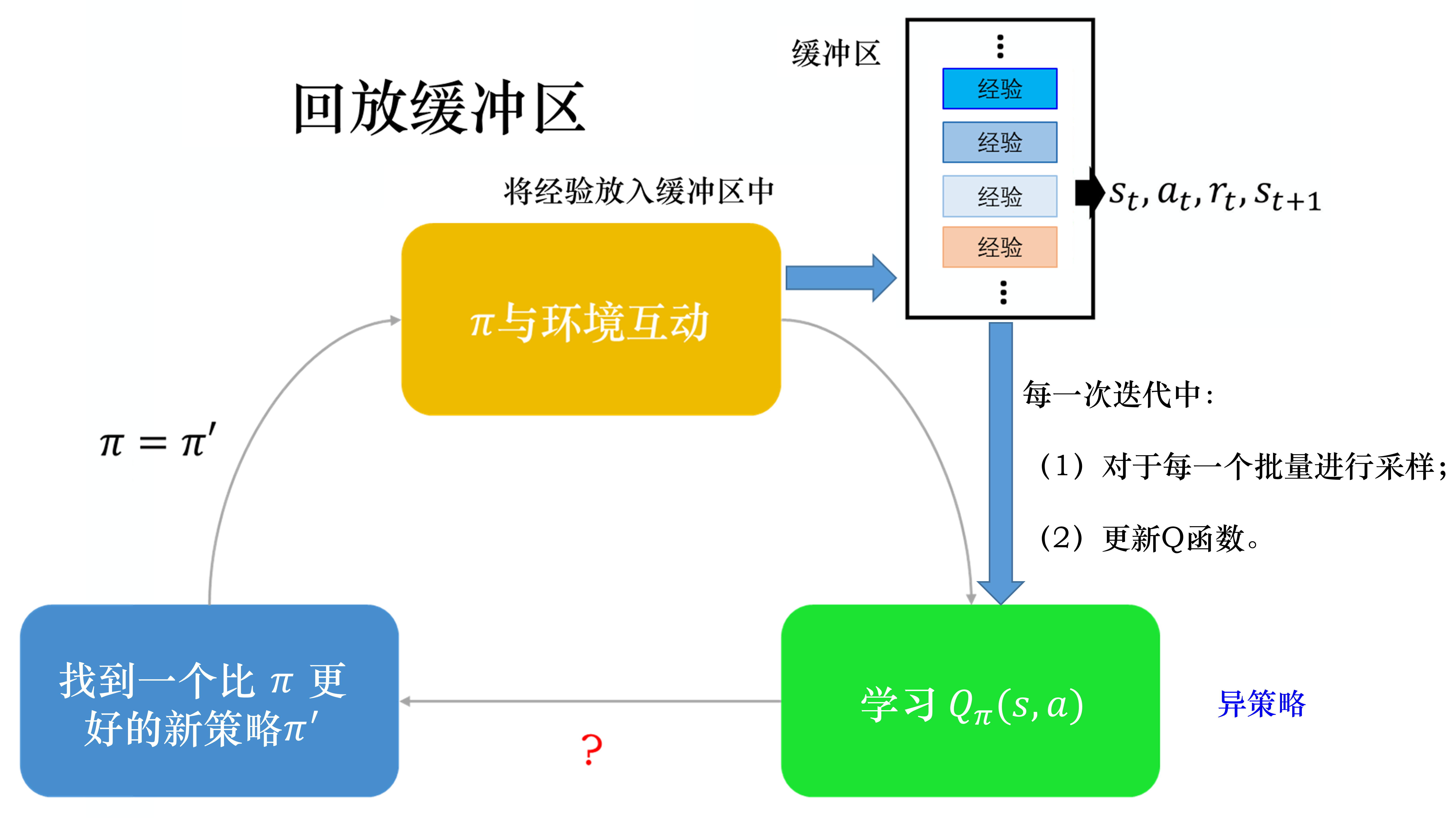经验回放可以设置一个缓冲区，存放过去的数据，里面可能包含不同策略的数据。
• 这样一方面增加了数据量；
• 同时也增加了数据的多样性。

因为时序差分法学习Q函数，所以即使是不同的策略也没有什么关系。

class ReplayBuffer:
    ''' 经验回放池 '''
    def __init__(self, capacity):
        self.buffer = collections.deque(maxlen=capacity)  # 队列,先进先出

    def add(self, state, action, reward, next_state, done):  # 将数据加入buffer
        self.buffer.append((state, action, reward, next_state, done))

    def sample(self, batch_size):  # 从buffer中采样数据,数量为batch_size
        transitions = random.sample(self.buffer, batch_size)
        state, action, reward, next_state, done = zip(*transitions)
        return np.array(state), action, reward, np.array(next_state), done

    def size(self):  # 目前buffer中数据的数量
        return len(self.buffer)

深度Q网络

将前面的思想融合就可以得到深度Q网络的算法

class Qnet(torch.nn.Module):
    ''' 只有一层隐藏层的Q网络 '''
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(Qnet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))  # 隐藏层使用ReLU激活函数
        return self.fc2(x)
        
class DQN:
    ''' DQN算法 '''
    def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma,
                 epsilon, target_update, device):
        self.action_dim = action_dim
        self.q_net = Qnet(state_dim, hidden_dim,
                          self.action_dim).to(device)  # Q网络
        # 目标网络
        self.target_q_net = Qnet(state_dim, hidden_dim,
                                 self.action_dim).to(device)
        # 使用Adam优化器
        self.optimizer = torch.optim.Adam(self.q_net.parameters(),
                                          lr=learning_rate)
        self.gamma = gamma  # 折扣因子
        self.epsilon = epsilon  # epsilon-贪婪策略
        self.target_update = target_update  # 目标网络更新频率
        self.count = 0  # 计数器,记录更新次数
        self.device = device

    def take_action(self, state):  # epsilon-贪婪策略采取动作
        if np.random.random() < self.epsilon:
            action = np.random.randint(self.action_dim)
        else:
            state = torch.tensor([state], dtype=torch.float).to(self.device)
            action = self.q_net(state).argmax().item()
        return action

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'],
                              dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
            self.device)
        rewards = torch.tensor(transition_dict['rewards'],
                               dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'],
                                   dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'],
                             dtype=torch.float).view(-1, 1).to(self.device)

        q_values = self.q_net(states).gather(1, actions)  # Q值
        # 下个状态的最大Q值
        max_next_q_values = self.target_q_net(next_states).max(1)[0].view(
            -1, 1)
        q_targets = rewards + self.gamma * max_next_q_values * (1 - dones
                                                                )  # TD误差目标
        dqn_loss = torch.mean(F.mse_loss(q_values, q_targets))  # 均方误差损失函数
        self.optimizer.zero_grad()  # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
        dqn_loss.backward()  # 反向传播更新参数
        self.optimizer.step()

        if self.count % self.target_update == 0:
            self.target_q_net.load_state_dict(
                self.q_net.state_dict())  # 更新目标网络
        self.count += 1

训练技巧

double DQN

在DQN中，当一个状态-动作对的值被高估了之后，会传导到使得其它的状态-动作对也被高估。

double DQN用一个网络来得到动作，用另一个网络来得到Q值，阻断被高估的Q值的传递。

class DQN:
    ''' DQN算法,包括Double DQN '''
    def __init__(...):
    def update(...):
        # 下个状态的最大Q值
        if self.dqn_type == 'DoubleDQN': # DQN与Double DQN的区别
            max_action = self.q_net(next_states).max(1)[1].view(-1, 1) 
            max_next_q_values = self.target_q_net(next_states).gather(1, max_action)
        else: # DQN的情况
            max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1)

Dueling DQN

Dueling DQN将网络的输出进行了拆分：
$$
Q(s,a) = V(s) + A(s,a)
$$
可以理解为拆分成了均值标量和动作效果向量：

• 即Q值一部分是由状态贡献；
• 另一部分是由采取的动作贡献。

通过这种方式类似于加入了先验知识：

• 一方面提升学习效率；
• 另一方面让模型对没有采取过的动作也有泛化能力。
• 在动作空间较大的环境下非常有效 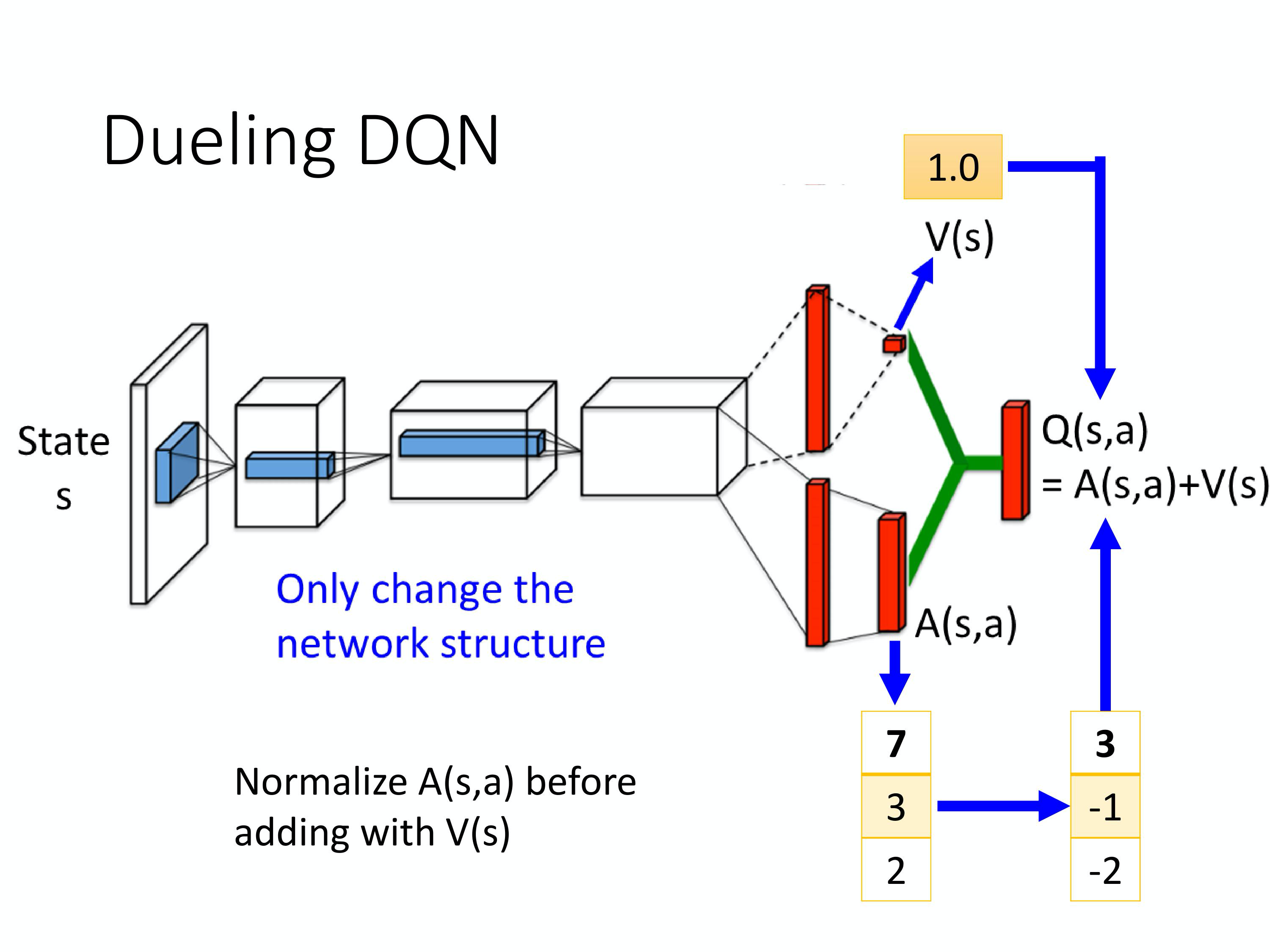为了防止模型不优化状态标量，可以对动作向量去均值。

class VAnet(torch.nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(VAnet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)  # 共享网络部分
        self.fc_A = torch.nn.Linear(hidden_dim, action_dim)
        self.fc_V = torch.nn.Linear(hidden_dim, 1)

    def forward(self, x):
        A = self.fc_A(F.relu(self.fc1(x)))
        V = self.fc_V(F.relu(self.fc1(x)))
        Q = V + A - A.mean(1).view(-1, 1)  # Q值由V值和A值计算得到
        return Q

Prioritized Experience Replay

在数据采样的时候从均匀采样改为按概率采样，给时序差分误差较大的样本更多权重。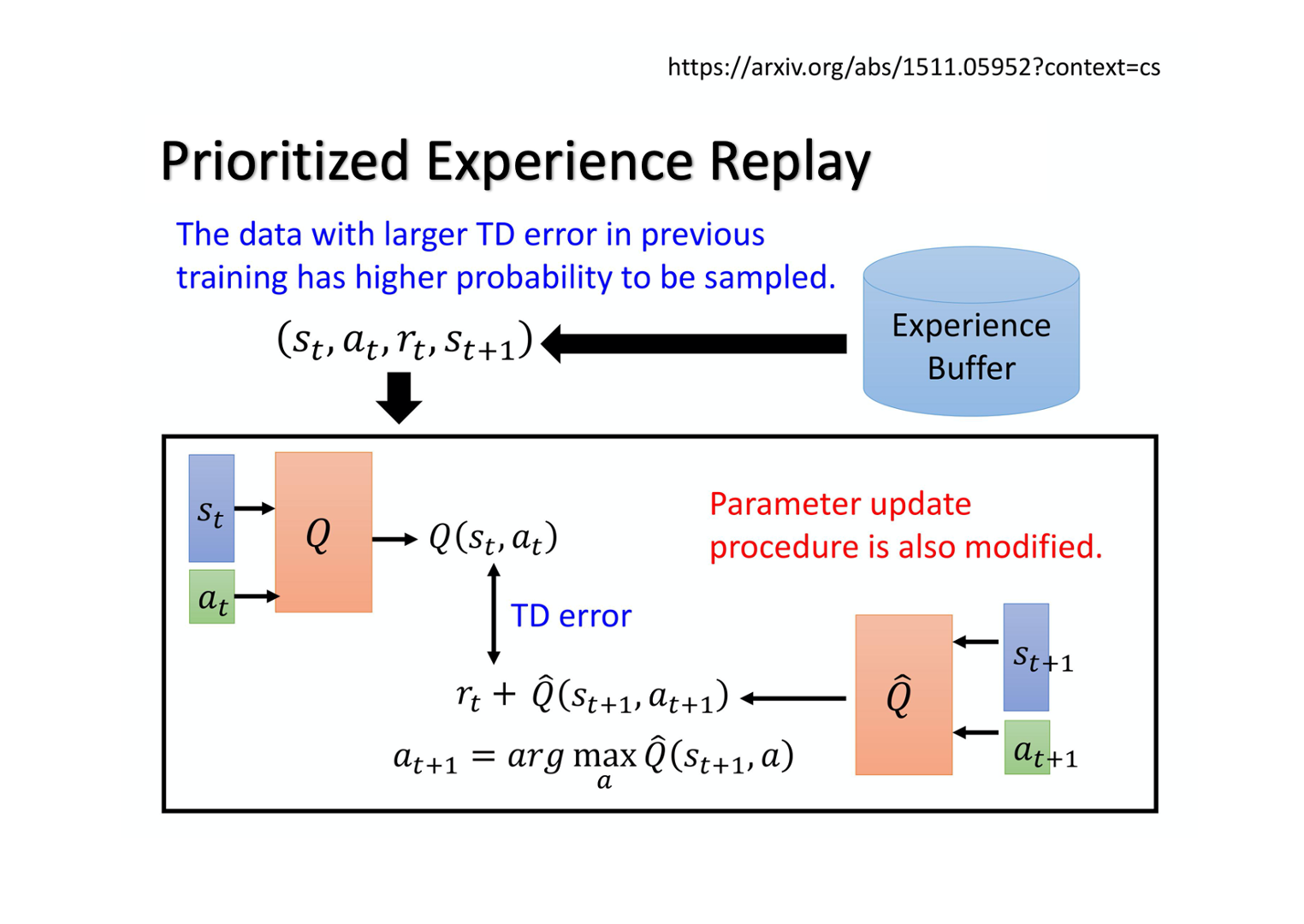

Balance between MC and TD

在蒙特卡罗和时序差分之间做了一个折中：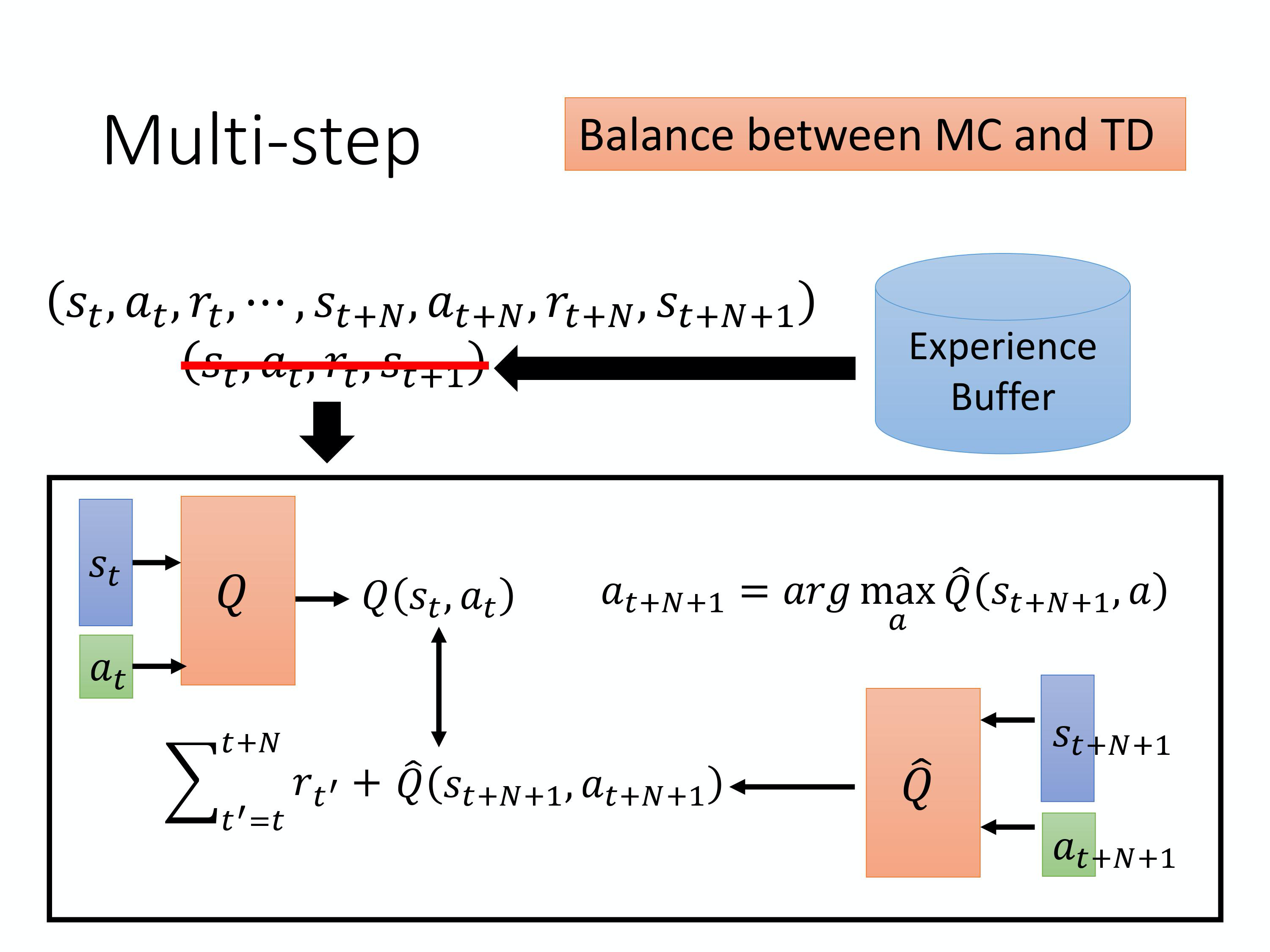

Noisy Net

在探索网络的参数上加噪声

在一个episode中探索网络的参数是固定了，随机也被固化下来，同一个状态会固定用同样的动作。
所以这种噪声是state-dependent exploration，而不像在动作上加噪声一样是随机乱试。

Distributional Q-function

又称C51，网络输出由各个动作的概率值变为各个动作的分布（包含动作取得各个收益的概率）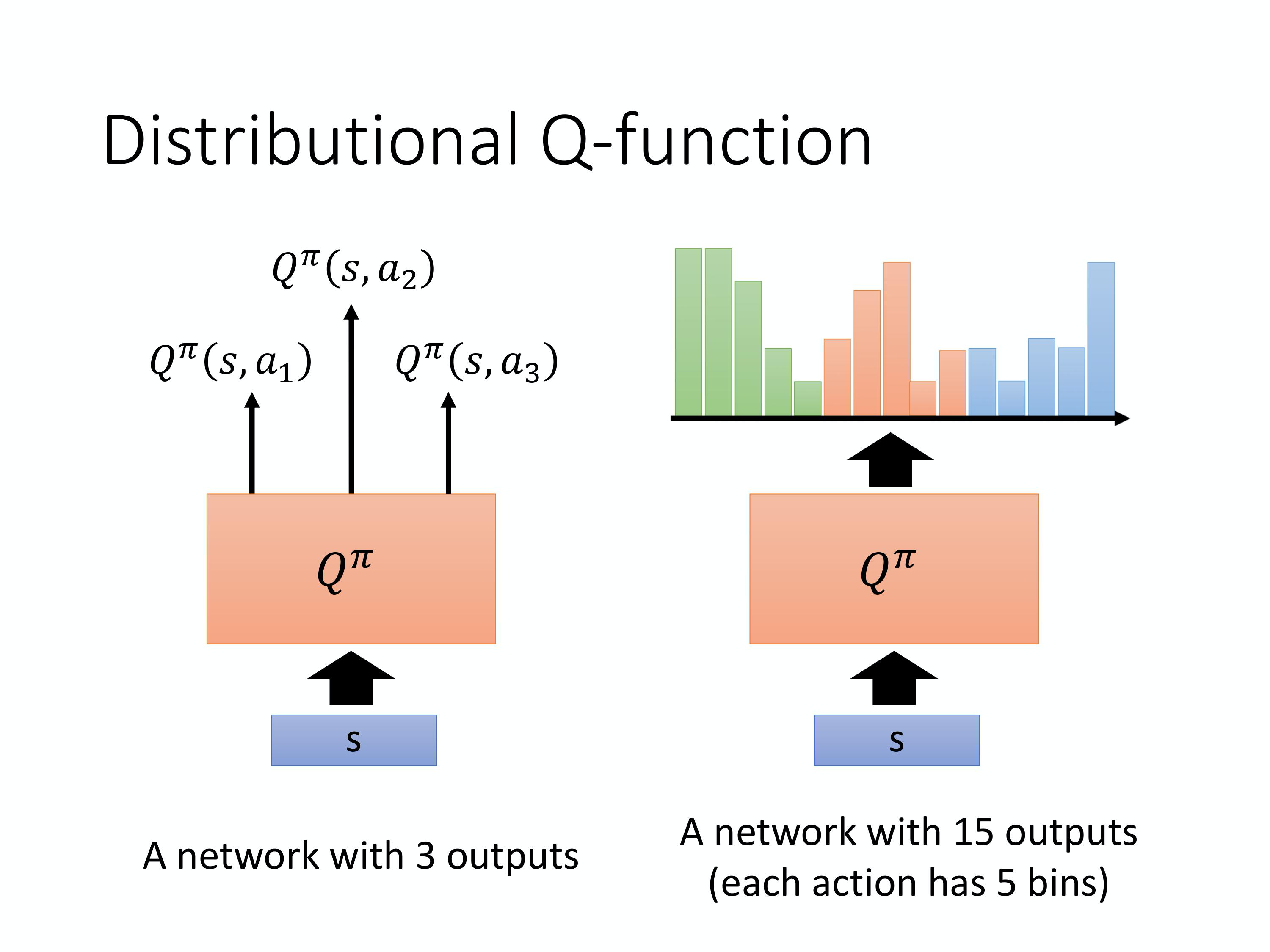

最后选动作的时候一般还是取平均收益最高的动作；
但是这个分布可以给训练和选择提供更多方案，例如判断风险。
同时也有防止高估状态值的效果。

Rainbow

将各个技巧融合所得
下图上面每一个是只用一个技巧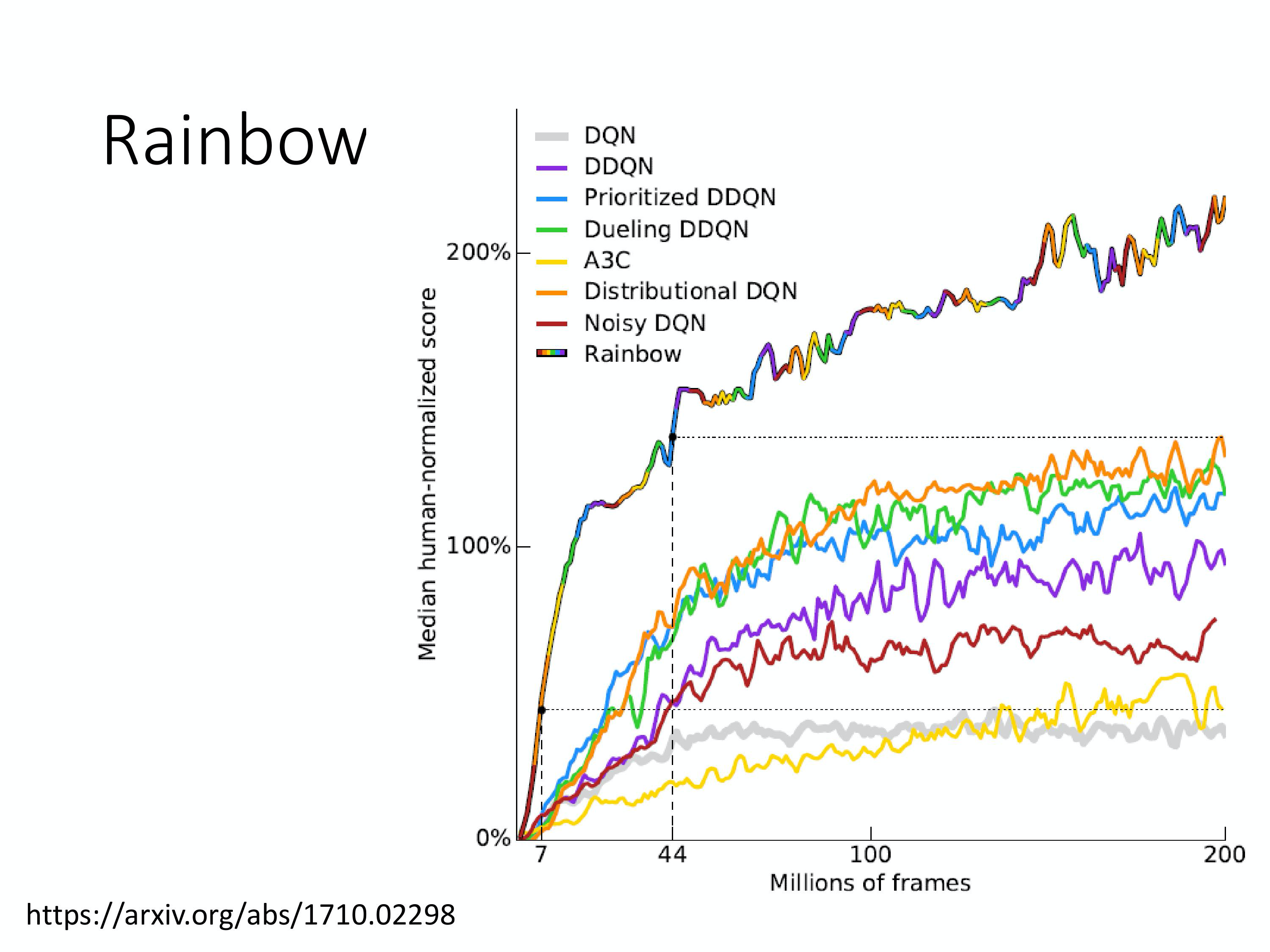

下图上面每一个是只去一个技巧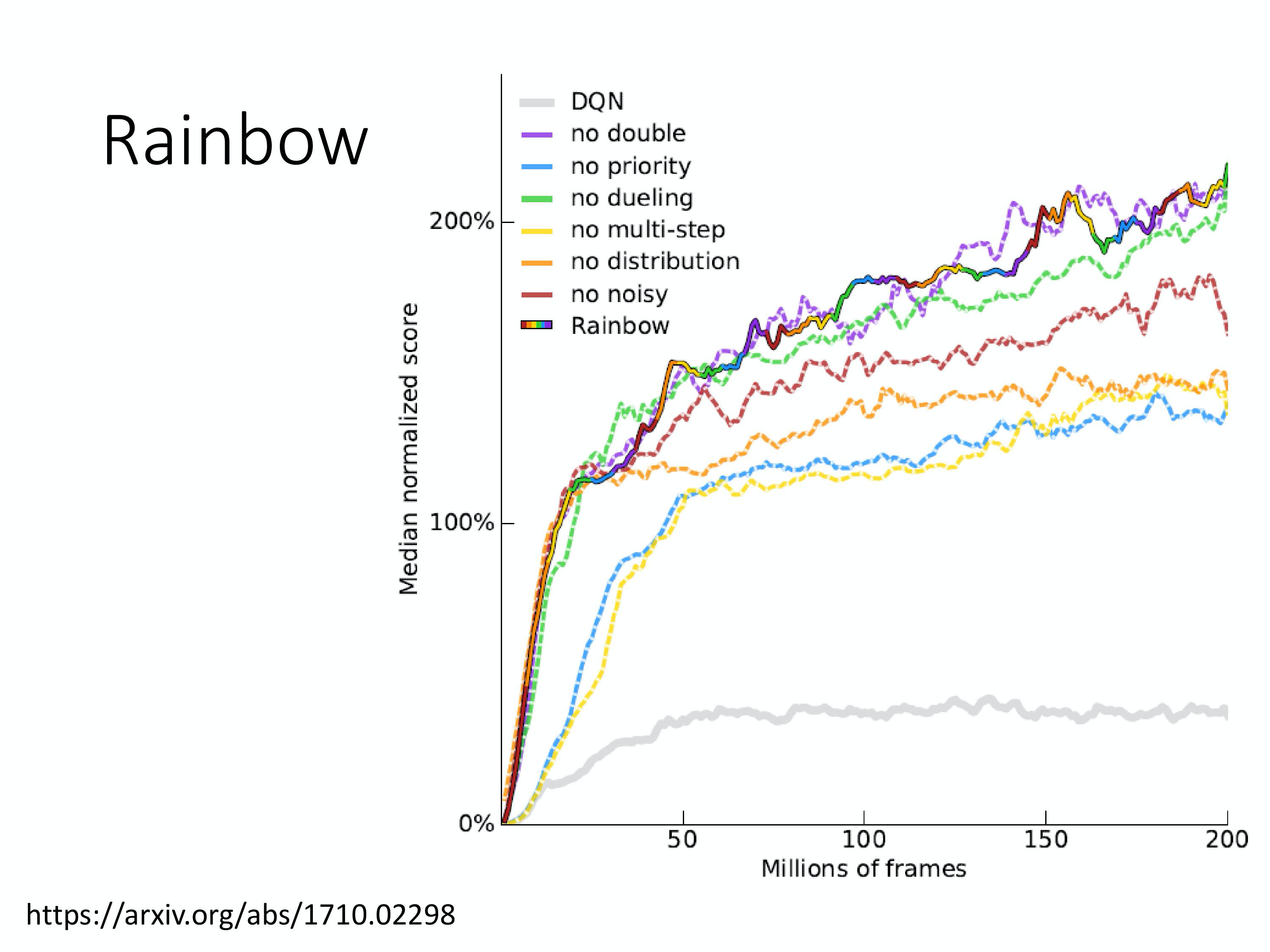

连续动作

设计网络

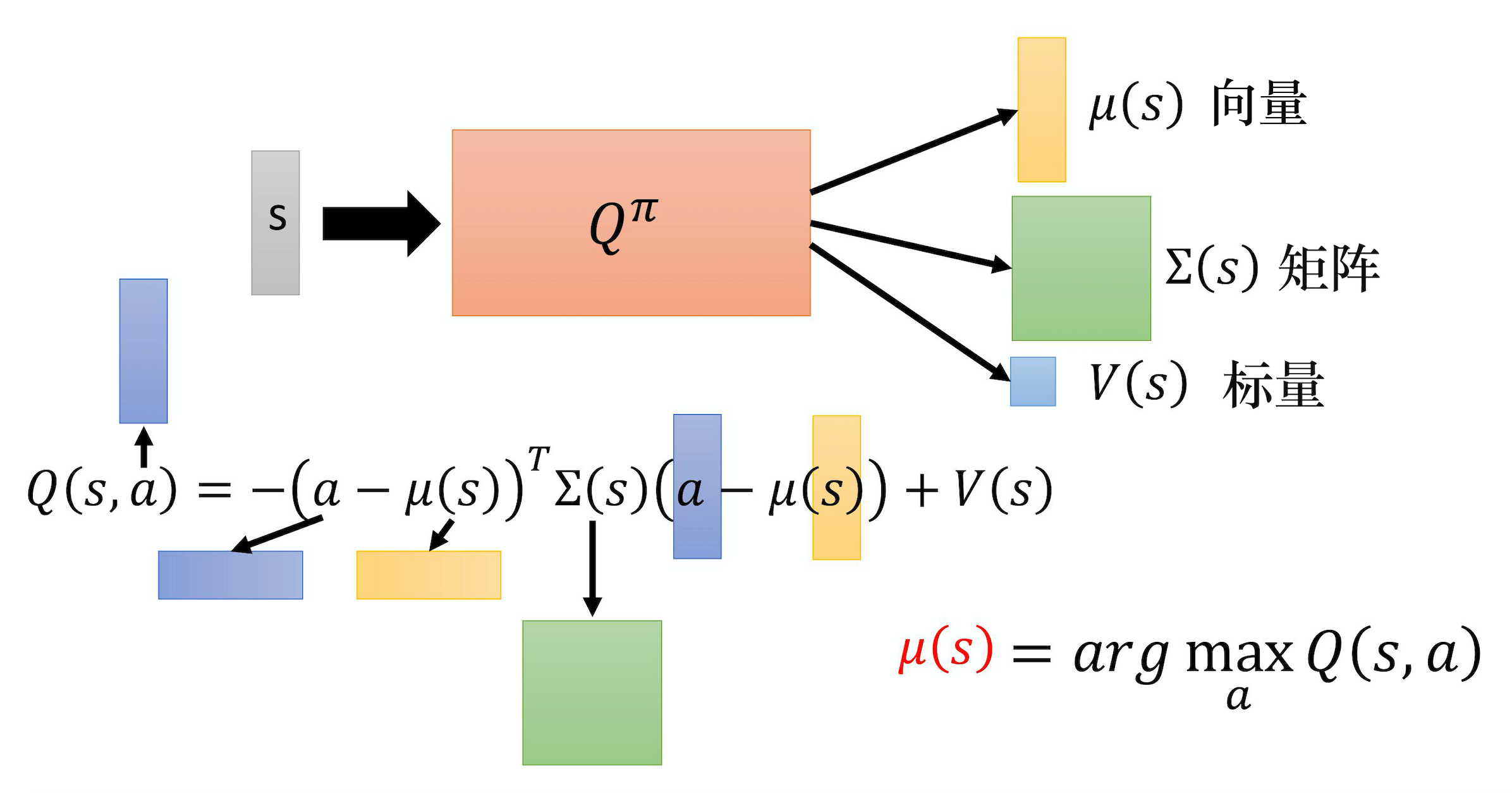让网络输出三个部分，其中均值$μ$就是能让Q值最大的动作，即： $$ \mu(s)=\arg \max_{a} Q(s, a) $$

Gorila

在DQN的基础上，提升并行能力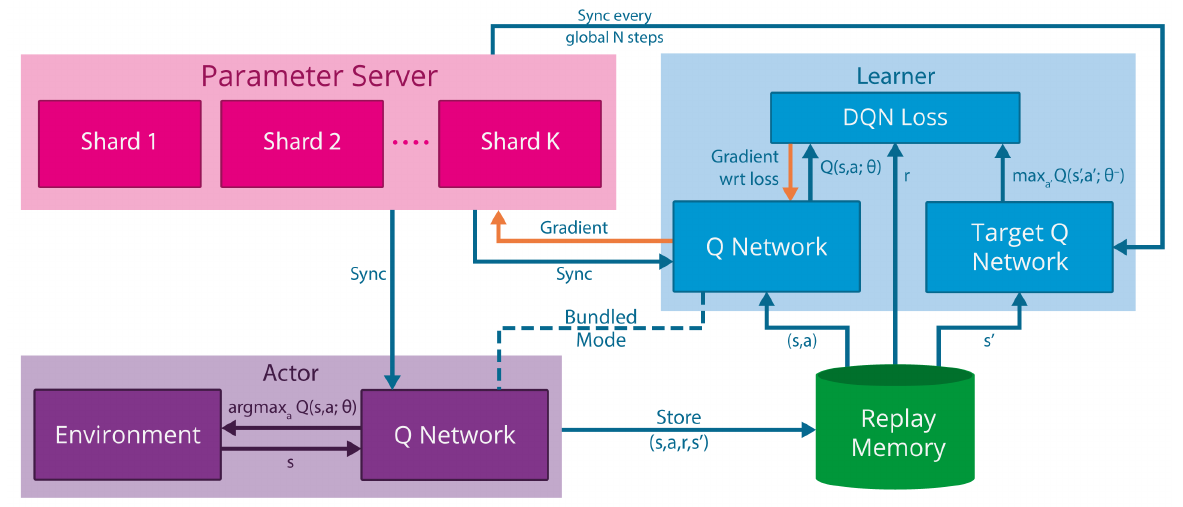

• 其中有actor, learner, parameter server和replay memory四个部分
• learner中对于Q网络的参数梯度会发给parameter server。
• Parameter server收到后以异步SGD的方式更新网络模型。
• 这个模型同步到actor中，actor基于该模型产生动作在环境中执行，产生的经验轨迹发往replay memory。
• Replay memory中的数据被learner采样拿去学习。
• Parameter server有多个的情况下，模型可被切成不相交的多份，分别放于多台机器上

基于策略

策略梯度

策略梯度计算

智能体与环境交互的轨迹为：
$$
\tau={s_{1}, a_{1}, s_{2}, a_{2}, \cdots, s_{t}, a_{t}}
$$
在参数为$\theta$的策略下轨迹的概率为：
$$
p_{\theta}(\tau) =p(s_{1}) p_{\theta}(a_{1} | s_{1}) p(s_{2} | s_{1}, a_{1}) p_{\theta}(a_{2} | s_{2}) p(s_{3} | s_{2}, a_{2}) \cdots \\
=p(s_{1}) \prod_{t=1}^{T} p_{\theta}(a_{t} | s_{t}) p(s_{t+1} | s_{t}, a_{t})
$$
其中$p(s_{t+1}|s_t,a_t)$是环境，无法控制；
而$p_\theta(a_t|s_t)$代表参数为$\theta$的智能体策略，是可以调整的。
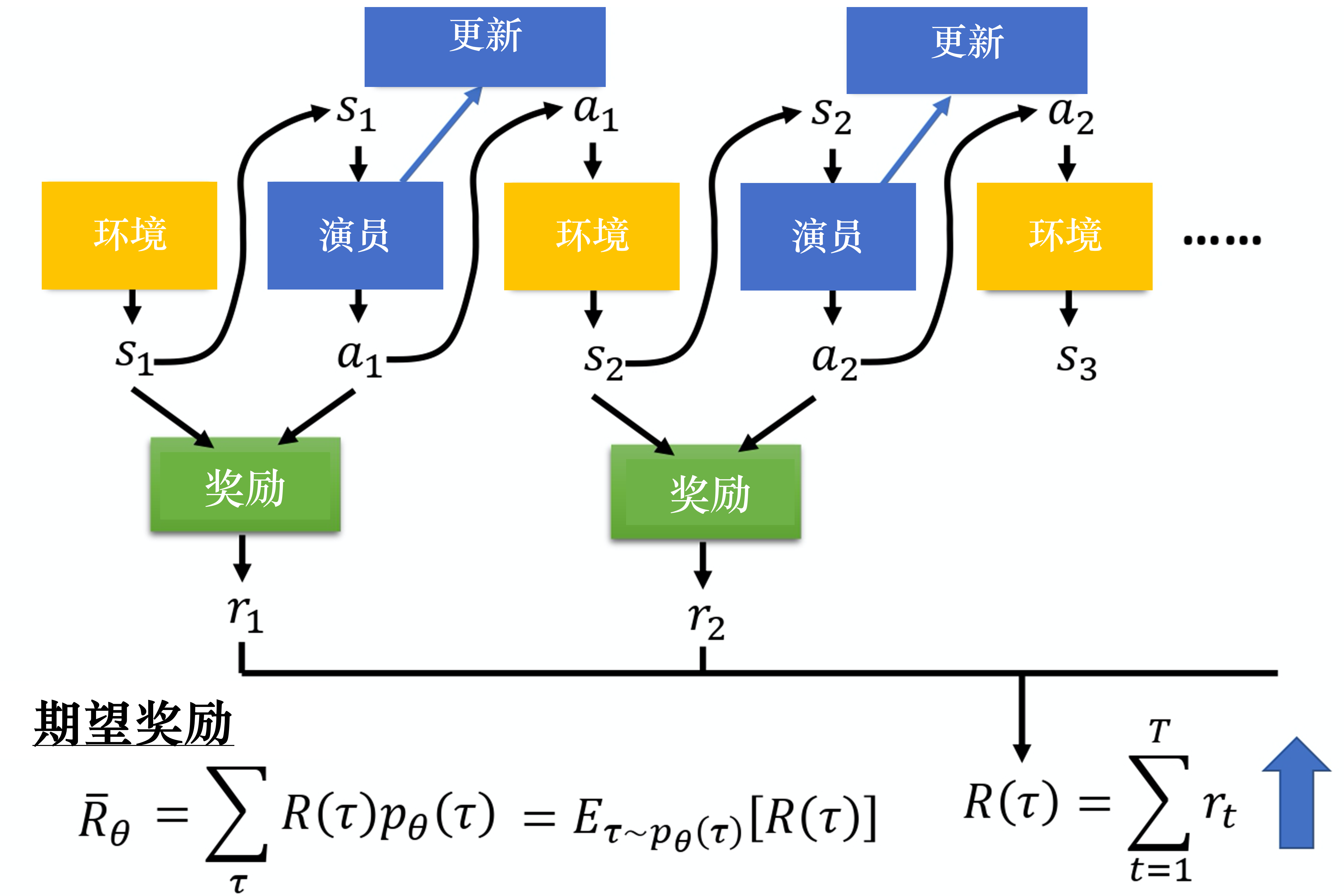
在不同的轨迹下会有不同的奖励$R(\tau)$，而它的期望也就是在参数为$\theta$的智能体策略下的奖励期望：
$$
R_{\theta}=\sum_{\tau} R(\tau) p_{\theta}(\tau)
$$

想要让奖励越大越好，可以使用梯度上升来最大化期望奖励：
$$
R_{\theta}=\sum_{\tau} R(\tau) p_{\theta}(\tau)
$$

即更新策略中的参数。
通过推导可得：

$$
\nabla R_{\theta}=\sum_{\tau} R(\tau) \nabla p_{\theta}(\tau) \\
=\sum_{\tau} R(\tau) p_{\theta}(\tau) \frac{\nabla p_{\theta}(\tau)}{p_{\theta}(\tau)} \\
=\sum_{\tau} R(\tau) p_{\theta}(\tau) \nabla \log p_{\theta}(\tau) \\
=E_{\tau \sim p_{\theta}(\tau)}[R(\tau) \nabla \log p_{\theta}(\tau)]\\
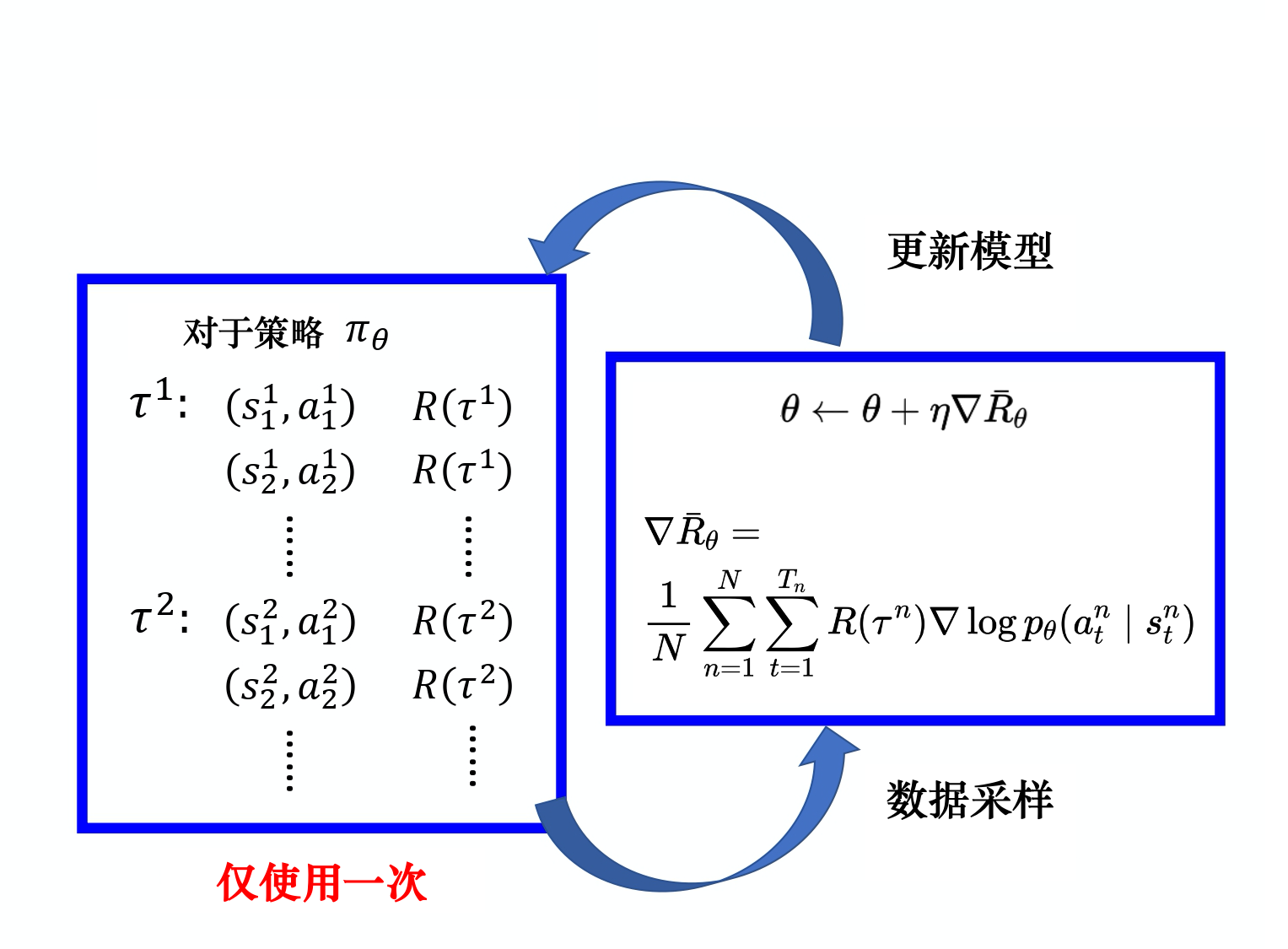
\approx \frac{1}{N} \sum_{n=1}^{N} R(\tau^{n}) \nabla \log p_{\theta}(\tau^{n}) \\
=\frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_{n}} R(\tau^{n}) \nabla \log p_{\theta}(a_{t}^{n} \mid s_{t}^{n})
$$

从公式可以直观看出：
当在状态$s_{t}$下采取动作$a_{t}$得到的奖励$\tau$是正的时候，就会增大在状态$s_{t}$下采取动作$a_{t}$的概率，反之减小概率；
同时当奖励越大时，也会以更大幅度来增大在状态$s_{t}$下采取动作$a_{t}$的概率。
这里的梯度上升也可以用深度学习的优化器：
$$
\theta \leftarrow \theta+\eta R_{\theta}
$$

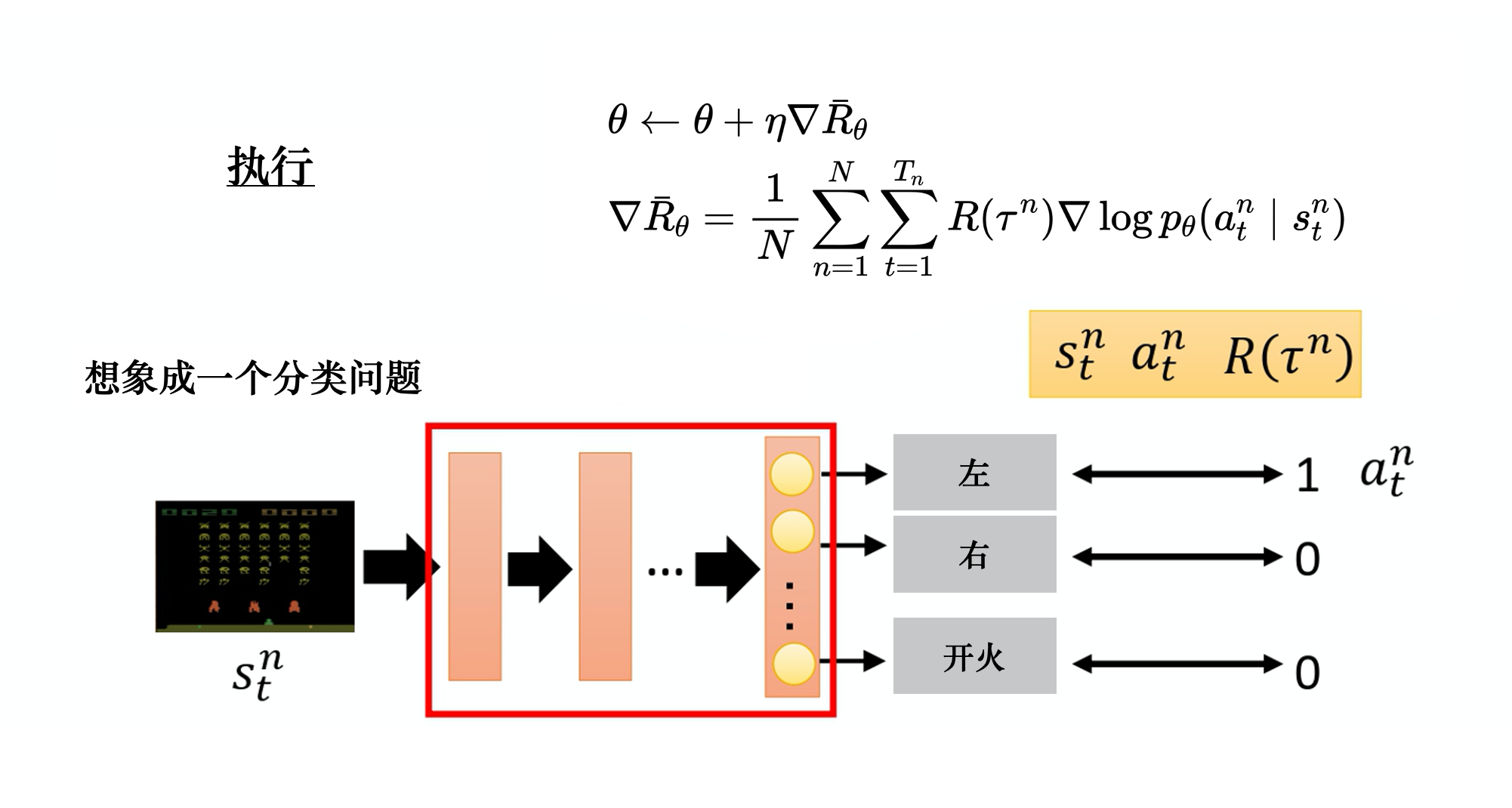
从网络结构的角度看，策略梯度和DQN可以非常相似：

• 网络结构都可以是输入状态，并给每个动作输出一个值
  • DQN还可以是输入状态和动作，输出一个值；策略梯度可以输出一个连续动作值
• 都是选择输出值最大的动作
• 优化都会使好的动作的值更大

实现技巧

添加基线

在有的环境中，奖励永远都是正，会使得采样到的动作的概率都会上升，而没有采样到的动作概率会下降，但没有采样到的动作不一定是不好的动作。
因此可以增加一个基线，使得奖励低于基线的动作概率下降：
$$
R_{\theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_{n}}(R(\tau^{n})-b) \log p_{\theta}(a_{t}^{n} \mid s_{t}^{n})
$$
基线可以采用奖励的平均值（期望值），也可以采用网络估计，让网络根据状态估计。这样$R-b$这一项就可以表示在某个状态下采取某个动作的相对优势，即采取这个动作是不是比采取别的动作好，也就是评论员（critic）。

调整奖励分数

前面给每个动作对都使用整个轨迹的奖励，而这是不合理的：

• 后面的动作对前面获得的奖励应该没有贡献；
• 现在的动作对未来的奖励的贡献应该衰减。
  应对第一个问题，可以加上时间限制，每个动作只用现在到未来的奖励：
  $$
  R_{\theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_{n}}(\sum_{t^{\prime}=t}^{T_{n}} r_{t^{\prime}}^{n}-b) \log p_{\theta}(a_{t}^{n} \mid s_{t}^{n})
  $$
  应对第二个问题，可以加上折扣系数

$$
R_{\theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_{n}}(\sum_{t^{\prime}=t}^{T_{n}} \gamma^{t^{\prime}-t} r_{t^{\prime}}^{n}-b) \log p_{\theta}(a_{t}^{n} \mid s_{t}^{n})
$$

REINFORCE

基于策略梯度的强化学习的经典算法，采用回合更新的模式：

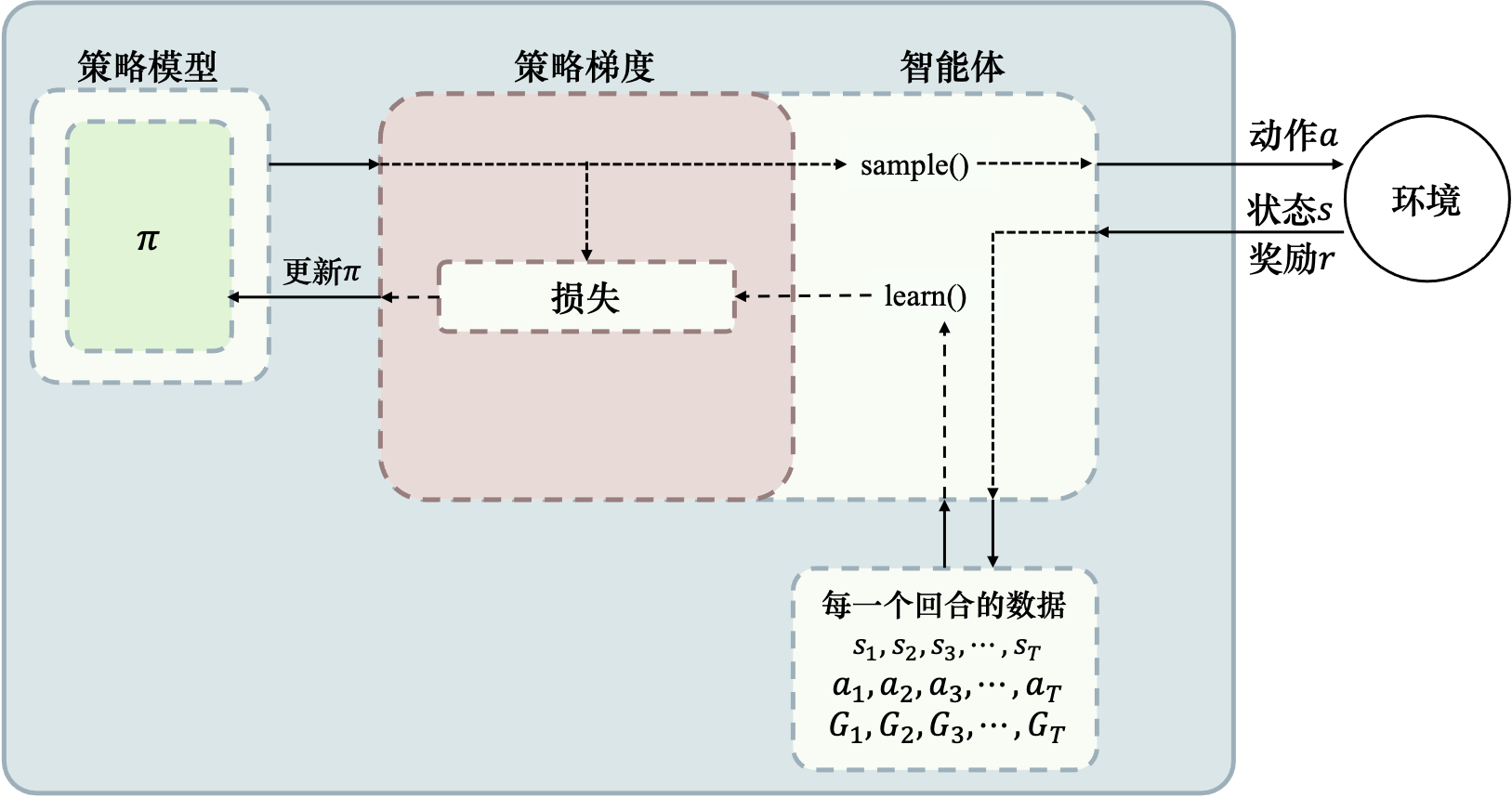
class PolicyNet(torch.nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(PolicyNet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        return F.softmax(self.fc2(x), dim=1)

class REINFORCE:
    def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma,
                 device):
        self.policy_net = PolicyNet(state_dim, hidden_dim,
                                    action_dim).to(device)
        self.optimizer = torch.optim.Adam(self.policy_net.parameters(),
                                          lr=learning_rate)  # 使用Adam优化器
        self.gamma = gamma  # 折扣因子
        self.device = device

    def take_action(self, state):  # 根据动作概率分布随机采样
        state = torch.tensor([state], dtype=torch.float).to(self.device)
        probs = self.policy_net(state)
        action_dist = torch.distributions.Categorical(probs)
        action = action_dist.sample()
        return action.item()

    def update(self, transition_dict):
        reward_list = transition_dict['rewards']
        state_list = transition_dict['states']
        action_list = transition_dict['actions']
        G = 0
        self.optimizer.zero_grad()
        for i in reversed(range(len(reward_list))):  # 从最后一步算起
            reward = reward_list[i]
            state = torch.tensor([state_list[i]],
                                 dtype=torch.float).to(self.device)
            action = torch.tensor([action_list[i]]).view(-1, 1).to(self.device)
            log_prob = torch.log(self.policy_net(state).gather(1, action))
            G = self.gamma * G + reward
            loss = -log_prob * G  # 每一步的损失函数
            loss.backward()  # 反向传播计算梯度
        self.optimizer.step()  # 梯度下降

演员-评论员（AC）

结合介于策略和基于价值的方法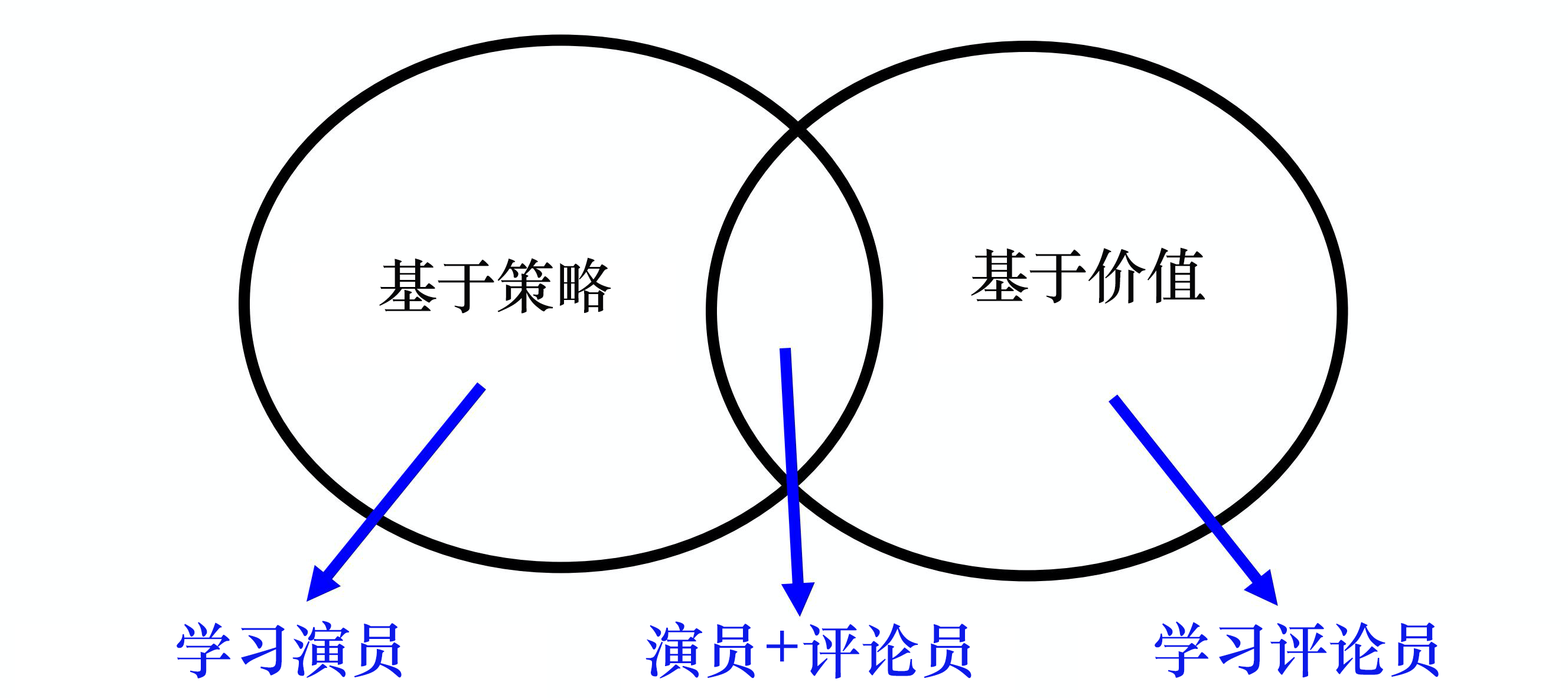

Actor-Critic优点：

1. 相比以值函数为中心的算法，Actor - Critic应用了策略梯度的做法，这能让它在连续动作或者高维动作空间中选取合适的动作，而 Q-learning 做这件事会很困难甚至瘫痪。另一方面，由Actor决定动作，相比只使用Critic的方法，增加了随机性、探索性，可以更好地找到更优解。
2. 相比单纯策略梯度，Actor - Critic应用了Q-learning或其他策略评估的做法，使得Actor Critic能进行单步更新而不是回合更新，比单纯的Policy Gradient的效率要高。

优势演员-评论员算法（A2C）

演员-评论员算法是一种结合策略梯度和时序差分学习的强化学习方法，其中，演员是指策略函数$\pi_{\theta}(a|s)$，即学习一个策略以得到尽可能高的回报。评论员是指价值函数$V_{\pi}(s)$，对当前策略的值函数进行估计，即评估演员的好坏。借助于价值函数，演员-评论员算法可以进行单步参数更新，不需要等到回合结束才进行更新。优势演员-评论员（advantage actor-critic，A2C）算法是将策略梯度的累计奖励改为了优势值。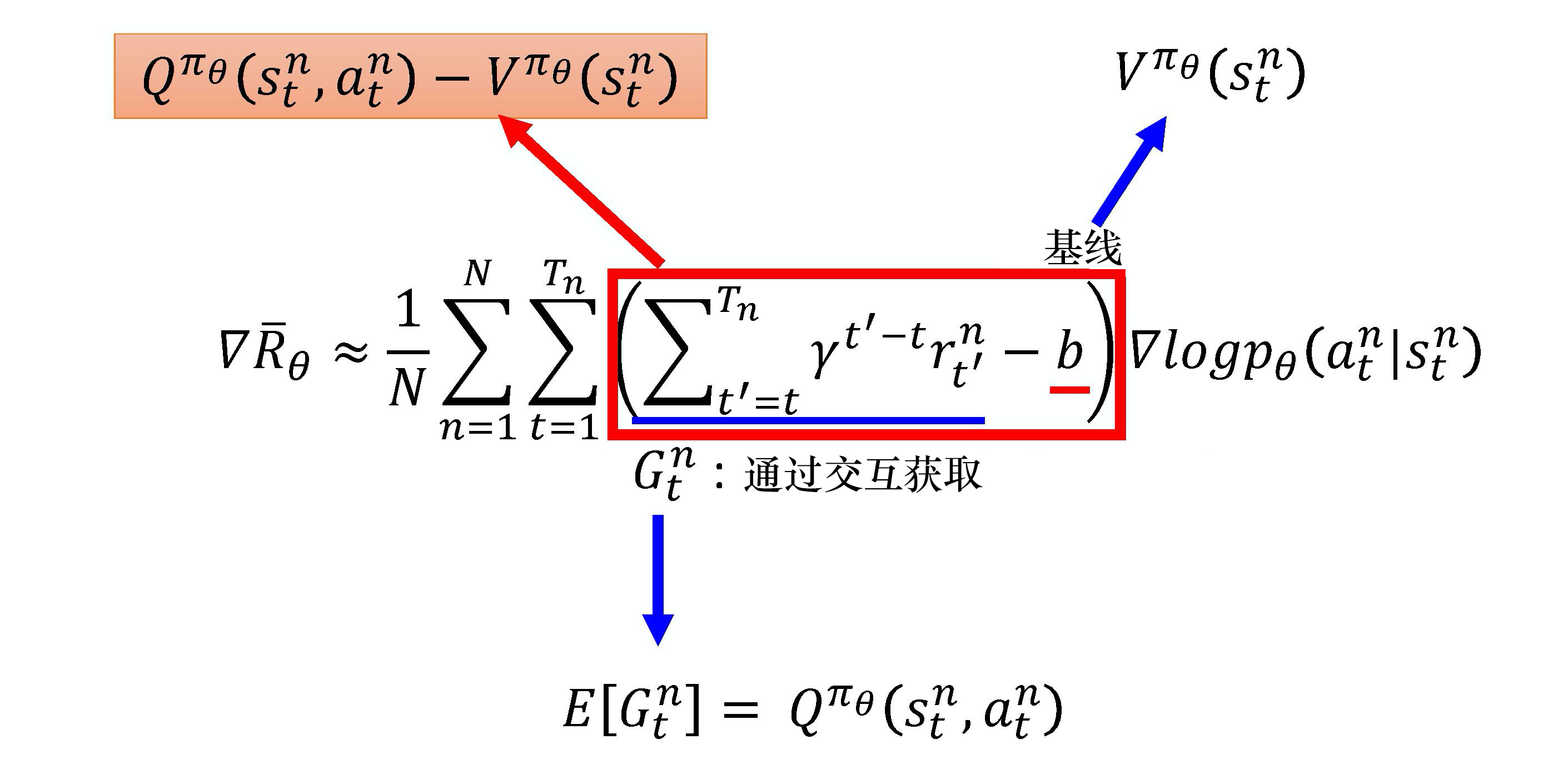

基本做法就是把策略梯度算法的累计奖励替换成价值函数，基本的价值函数有$V_{\pi_{\theta}}(s_{t}^{n})$和$Q_{\pi_{\theta}}(s_{t}^{n}, a_{t}^{n})$，还可以替换成优势函数$Q_{\pi_{\theta}}(s_{t}^{n}, a_{t}^{n})-V_{\pi_{\theta}}(s_{t}^{n})$。后者就是优势演员-评论员（advantage actor-critic，A2C）算法。
而A2C的公式也可以简化成只用一个网络：
$$
Q_{\pi_{\theta}}(s_{t}^{n}, a_{t}^{n})-V_{\pi_{\theta}}(s_{t}^{n})\\
=\mathbb{E}[r_{t}^{n}+\gamma V_{\pi}(s_{t+1}^{n})]-V_{\pi_{\theta}}(s_{t}^{n})\\
=r_{t}^{n}+\gamma V_{\pi}(s_{t+1}^{n})-V_{\pi_{\theta}}(s_{t}^{n})
$$
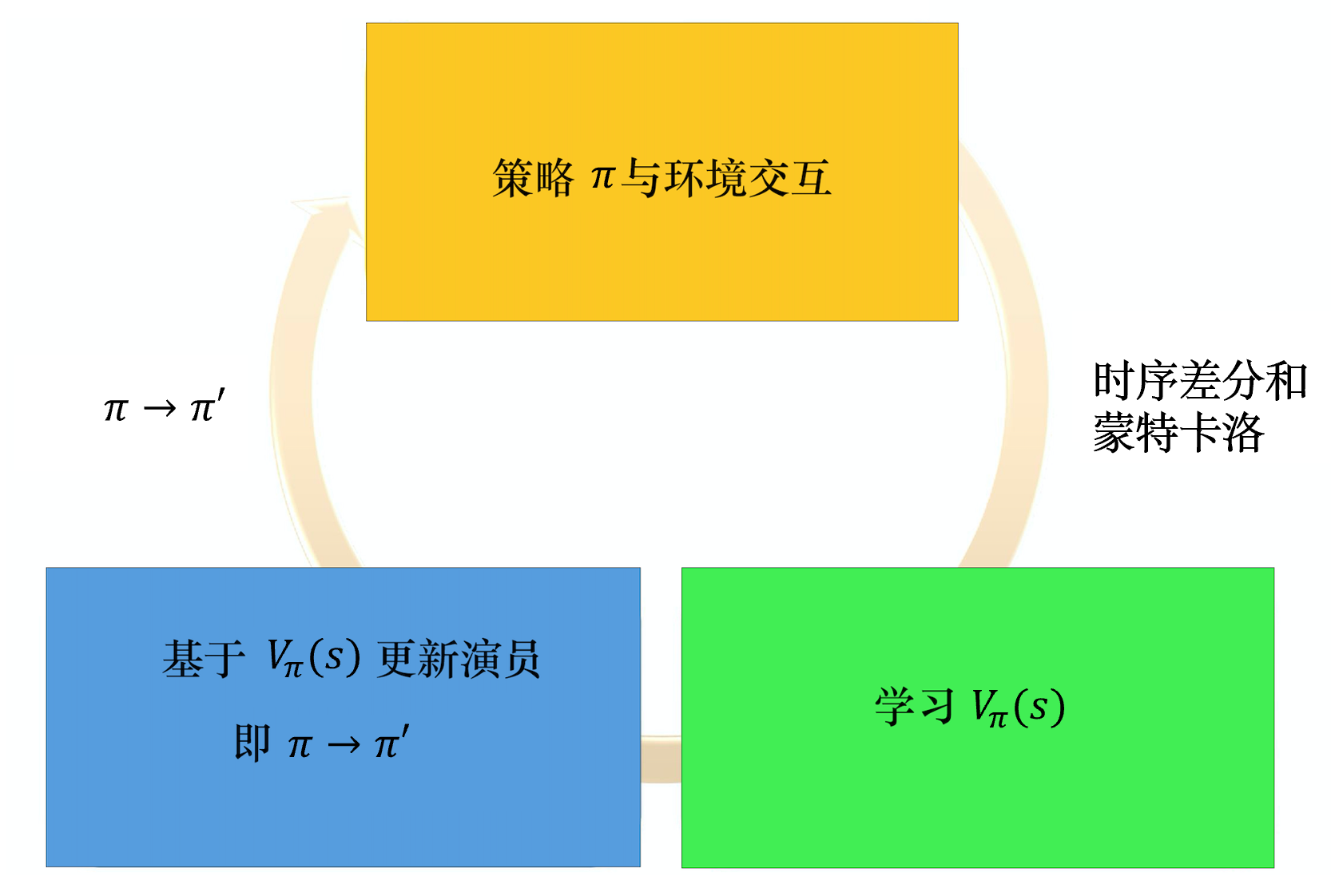
在训练的时候，演员和评论家是交替进行优化的。
所以策略梯度为：
$$
\nabla \bar{R}{\theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_{n}}\left(r_{t}^{n}+\gamma V^{\pi}\left(s_{t+1}^{n}\right)-V^{\pi}\left(s_{t}^{n}\right)\right) \nabla \log p_{\theta}\left(a_{t}^{n} \mid s_{t}^{n}\right)
$$

因为演员和评论员的输入都是状态，所以这两个网络可以考虑共享底层网络来提升泛化性，降低训练难度。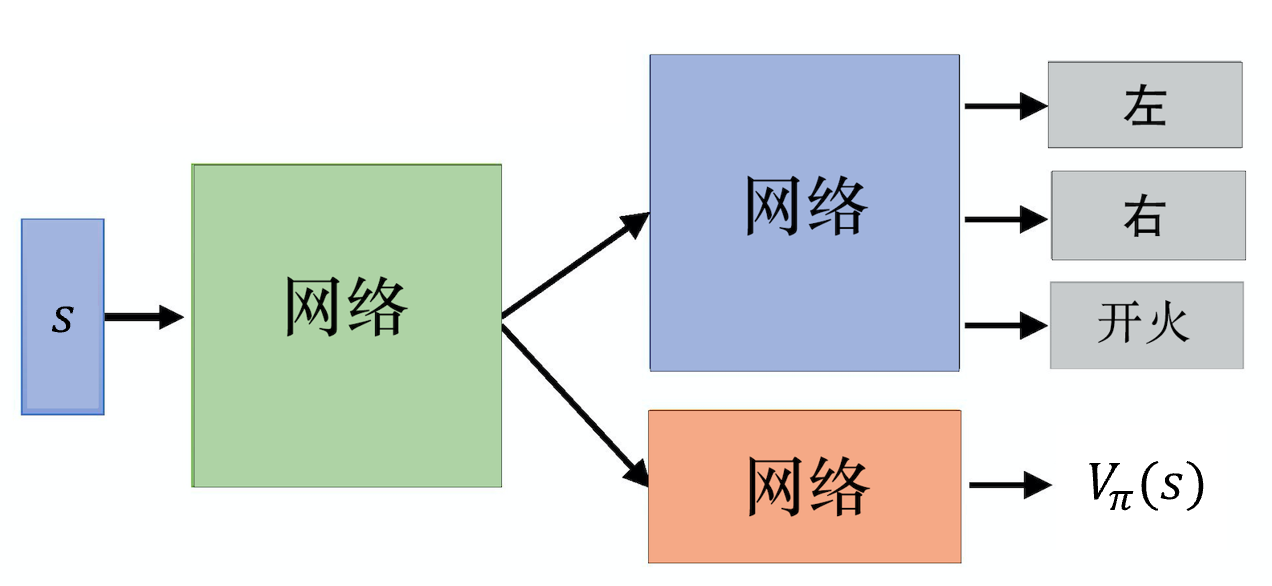

还可以对策略的输出分布加以限制，让分布的熵不要太小，以增加探索性。

class PolicyNet(torch.nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(PolicyNet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        return F.softmax(self.fc2(x), dim=1)

class ValueNet(torch.nn.Module):
    def __init__(self, state_dim, hidden_dim):
        super(ValueNet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, 1)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        return self.fc2(x)

class ActorCritic:
    def __init__(self, state_dim, hidden_dim, action_dim, actor_lr, critic_lr,
                 gamma, device):
        # 策略网络
        self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
        self.critic = ValueNet(state_dim, hidden_dim).to(device)  # 价值网络
        # 策略网络优化器
        self.actor_optimizer = torch.optim.Adam(self.actor.parameters(),
                                                lr=actor_lr)
        self.critic_optimizer = torch.optim.Adam(self.critic.parameters(),
                                                 lr=critic_lr)  # 价值网络优化器
        self.gamma = gamma
        self.device = device

    def take_action(self, state):
        state = torch.tensor([state], dtype=torch.float).to(self.device)
        probs = self.actor(state)
        action_dist = torch.distributions.Categorical(probs)
        action = action_dist.sample()
        return action.item()

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'],
                              dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
            self.device)
        rewards = torch.tensor(transition_dict['rewards'],
                               dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'],
                                   dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'],
                             dtype=torch.float).view(-1, 1).to(self.device)

        # 时序差分目标
        td_target = rewards + self.gamma * self.critic(next_states) * (1 -
                                                                       dones)
        td_delta = td_target - self.critic(states)  # 时序差分误差
        log_probs = torch.log(self.actor(states).gather(1, actions))
        actor_loss = torch.mean(-log_probs * td_delta.detach())
        # 均方误差损失函数
        critic_loss = torch.mean(
            F.mse_loss(self.critic(states), td_target.detach()))
        self.actor_optimizer.zero_grad()
        self.critic_optimizer.zero_grad()
        actor_loss.backward()  # 计算策略网络的梯度
        critic_loss.backward()  # 计算价值网络的梯度
        self.actor_optimizer.step()  # 更新策略网络的参数
        self.critic_optimizer.step()  # 更新价值网络的参数

异步优势演员-评论员算法（A3C）

为了提升训练速度，可以采用多进程的方式，每个子进程探索一个环境，并把得到的梯度回传给主节点更新参数：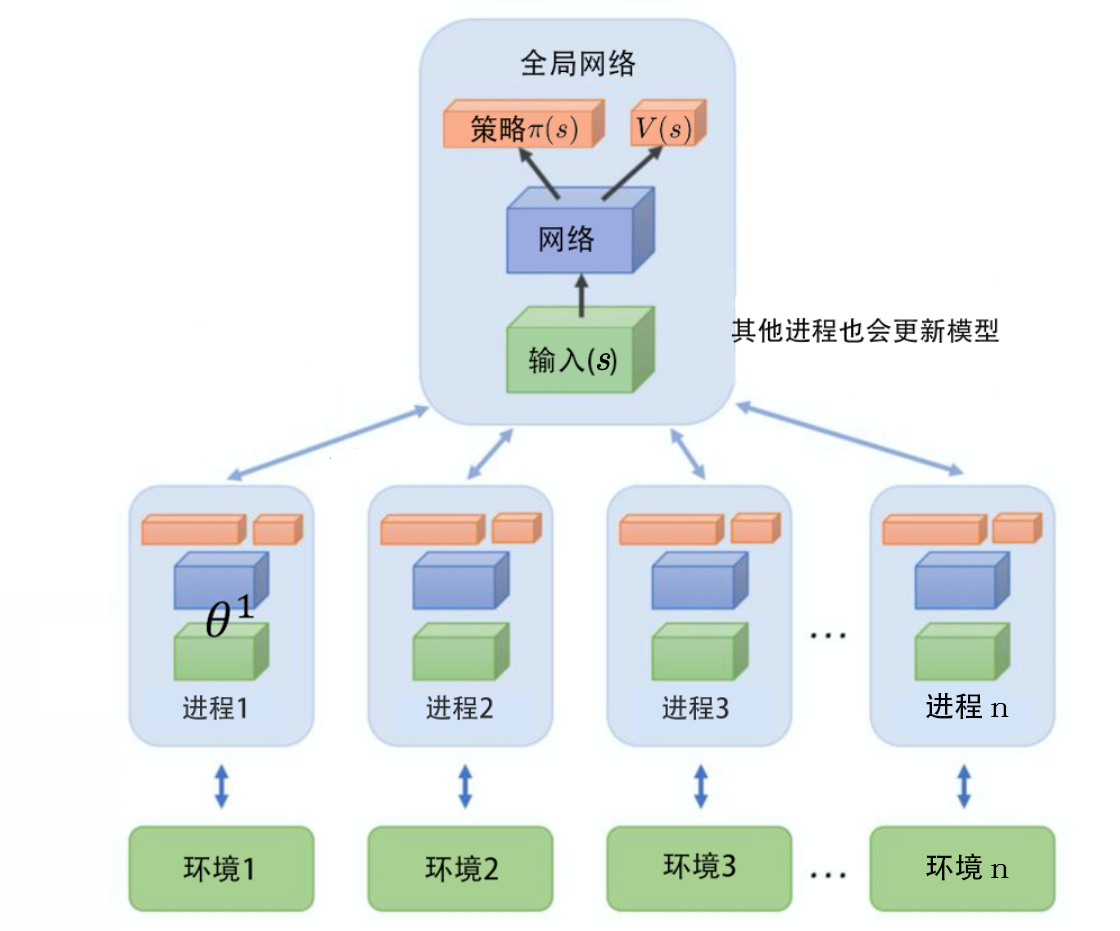

主节点将子进程的梯度进行平均并回传新的参数给各个节点
因为各个子进程异步进行，因此对GPU的利用效率不高

IMPALA

• 每个actor起一个模拟环境，定期从learner获取最新的神经网络参数，来使用自己能获得的最新策略去采样，并且把获取到的数据传回供learner去更新各个神经网络参数。
• learner通过获取actor得到的轨迹来做SGD来更新各个神经网络的参数
• learner使用GPU，actor使用CPU
• 当训练规模扩大的时候，可以使用多个learner（多块GPU）并且每块GPU配套多个actor（CPU）。每个learner只从自己的actor们中获取样本进行更新，learner之间定期交换gradient并且更新网络参数，actor也定期从任意learner上获取并更新神经网络参数。
• 还通过V-trace来减弱了因为off-policy带来的不稳定性

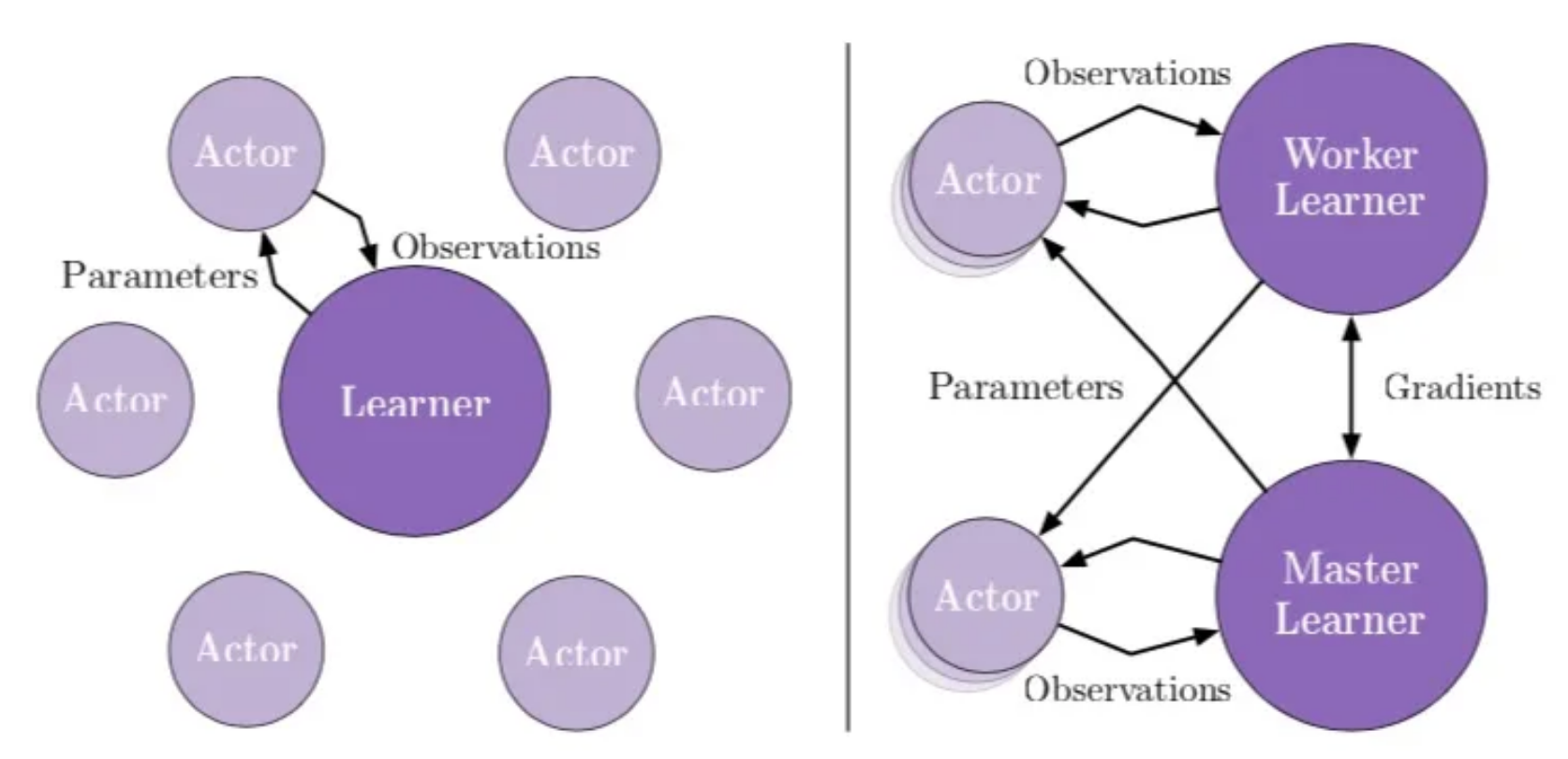
• actor和learner相互异步工作，极大提高了时间利用率；
• actor传输的是数据而非梯度，因此通信开销更小；
• 相比于A3C和batched A2C，具有更好的高性能计算性能；
• 单任务训练上相比于分布式A3C、单机A3C和batched A2C有更好的性能，并且对于超参数更稳定；

路径衍生策略梯度算法

优势演员-评论员算法中的Q网络只能评价动作好不好，不能提供好的方向，路径衍生策略梯度算法的思想类似于生成对抗网络，让Q网络同时输入状态和演员生成的动作，得到动作价值，进而可以给演员的优化提供方向。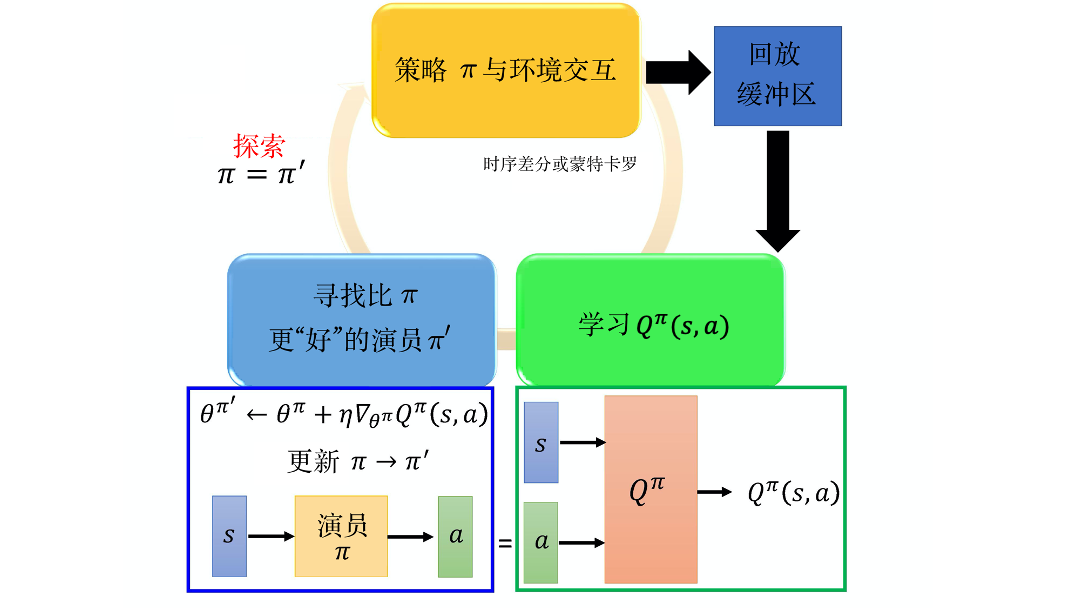

路径衍生策略梯度算法也可以看成是在深度Q网络的基础上用策略梯度来选择动作，以解决动作空间过大或者动作连续的问题：

与生成对抗网络在技巧上的研究

TRPO

Policy gradient是on-policy的做法，这样要收集很多数据，然后更新参数，再去收集数据，效率较低；
可以用一个policy去跟环境互动收集数据，另一个policy可以用收集到的数据执行梯度上升。
考虑到两个policy的参数不一样，动作分布不一样，因此梯度计算需要进行一些调整。
假设两个policy的差别不大的情况下，可以通过重要性采样，加入两个policy的概率值来调整：

其中跟环境互动收集数据的policy参数$\theta’$是常数，不用求梯度。

当两个policy的差别过大时，会使得算法过程不稳定，因此要控制这种差异：

• 一种思路是控制参数空间，控制参数更新量；
  • 但是步长过小会造成效率低下；
  • 步长过大算法就会不稳定；
  • 即无法找到好的固定步长
• 另一种思路是控制策略空间：
  • 让新旧策略在策略空间上的变化不大；

即使是on-policy做法，按照回合更新时，从后往前更新，也会出现策略不一致的情况

信任区域策略优化(Trust Region Policy Optimization，TRPO)在梯度公式的基础上通过KL散度来限制两个参数的差距：
$$
\begin{aligned}
J_{T R P O}^{\theta^{\prime}}(\theta)=E_{(s_{t}, a_{t}) \sim \pi_{\theta^{\prime}}}[\frac{p_{\theta}(a_{t} | s_{t})}{p_{\theta^{\prime}}(a_{t} | s_{t})} A^{\theta^{\prime}}(s_{t}, a_{t})] \ \
\mathrm{KL}(\theta, \theta^{\prime})<\delta
\end{aligned}
$$
这里的KL散度不是衡量参数的差异，而是衡量在相同状态下采取的行动差异。

GAE

在优势函数方面，TRPO和后续的PPO采用GAE(General Advantage Estimation)的方式。
它的公式为：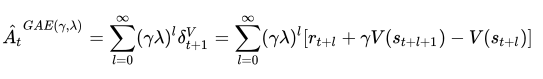

可以看成是另一种N步TD，$\lambda$等于0时，等效为A2C中的优势函数：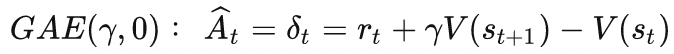

而当$\lambda$等于1时，则变成了使用轨迹终点来计算：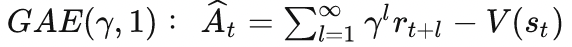

即$\gamma$和$\lambda$越小时，更多地使用较近的奖励，因而方差更小，同时偏差大；
反之$\gamma$和$\lambda$越大时，更多地使用较远的奖励，因而方差更大，同时偏差小；

class TRPO:
    """ TRPO算法 """
    def __init__(self, hidden_dim, state_space, action_space, lmbda,
                 kl_constraint, alpha, critic_lr, gamma, device):
        state_dim = state_space.shape[0]
        action_dim = action_space.n
        # 策略网络参数不需要优化器更新
        self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
        self.critic = ValueNet(state_dim, hidden_dim).to(device)
        self.critic_optimizer = torch.optim.Adam(self.critic.parameters(),
                                                 lr=critic_lr)
        self.gamma = gamma
        self.lmbda = lmbda  # GAE参数
        self.kl_constraint = kl_constraint  # KL距离最大限制
        self.alpha = alpha  # 线性搜索参数
        self.device = device

    def take_action(self, state):
        state = torch.tensor([state], dtype=torch.float).to(self.device)
        probs = self.actor(state)
        action_dist = torch.distributions.Categorical(probs)
        action = action_dist.sample()
        return action.item()

    def hessian_matrix_vector_product(self, states, old_action_dists, vector):
        # 计算黑塞矩阵和一个向量的乘积
        new_action_dists = torch.distributions.Categorical(self.actor(states))
        kl = torch.mean(
            torch.distributions.kl.kl_divergence(old_action_dists,
                                                 new_action_dists))  # 计算平均KL距离
        kl_grad = torch.autograd.grad(kl,
                                      self.actor.parameters(),
                                      create_graph=True)
        kl_grad_vector = torch.cat([grad.view(-1) for grad in kl_grad])
        # KL距离的梯度先和向量进行点积运算
        kl_grad_vector_product = torch.dot(kl_grad_vector, vector)
        grad2 = torch.autograd.grad(kl_grad_vector_product,
                                    self.actor.parameters())
        grad2_vector = torch.cat([grad.view(-1) for grad in grad2])
        return grad2_vector

    def conjugate_gradient(self, grad, states, old_action_dists):  # 共轭梯度法求解方程
        x = torch.zeros_like(grad)
        r = grad.clone()
        p = grad.clone()
        rdotr = torch.dot(r, r)
        for i in range(10):  # 共轭梯度主循环
            Hp = self.hessian_matrix_vector_product(states, old_action_dists,
                                                    p)
            alpha = rdotr / torch.dot(p, Hp)
            x += alpha * p
            r -= alpha * Hp
            new_rdotr = torch.dot(r, r)
            if new_rdotr < 1e-10:
                break
            beta = new_rdotr / rdotr
            p = r + beta * p
            rdotr = new_rdotr
        return x

    def compute_surrogate_obj(self, states, actions, advantage, old_log_probs,
                              actor):  # 计算策略目标
        log_probs = torch.log(actor(states).gather(1, actions))
        ratio = torch.exp(log_probs - old_log_probs)
        return torch.mean(ratio * advantage)

    def line_search(self, states, actions, advantage, old_log_probs,
                    old_action_dists, max_vec):  # 线性搜索
        old_para = torch.nn.utils.convert_parameters.parameters_to_vector(
            self.actor.parameters())
        old_obj = self.compute_surrogate_obj(states, actions, advantage,
                                             old_log_probs, self.actor)
        for i in range(15):  # 线性搜索主循环
            coef = self.alpha**i
            new_para = old_para + coef * max_vec
            new_actor = copy.deepcopy(self.actor)
            torch.nn.utils.convert_parameters.vector_to_parameters(
                new_para, new_actor.parameters())
            new_action_dists = torch.distributions.Categorical(
                new_actor(states))
            kl_div = torch.mean(
                torch.distributions.kl.kl_divergence(old_action_dists,
                                                     new_action_dists))
            new_obj = self.compute_surrogate_obj(states, actions, advantage,
                                                 old_log_probs, new_actor)
            if new_obj > old_obj and kl_div < self.kl_constraint:
                return new_para
        return old_para

    def policy_learn(self, states, actions, old_action_dists, old_log_probs,
                     advantage):  # 更新策略函数
        surrogate_obj = self.compute_surrogate_obj(states, actions, advantage,
                                                   old_log_probs, self.actor)
        grads = torch.autograd.grad(surrogate_obj, self.actor.parameters())
        obj_grad = torch.cat([grad.view(-1) for grad in grads]).detach()
        # 用共轭梯度法计算x = H^(-1)g
        descent_direction = self.conjugate_gradient(obj_grad, states,
                                                    old_action_dists)

        Hd = self.hessian_matrix_vector_product(states, old_action_dists,
                                                descent_direction)
        max_coef = torch.sqrt(2 * self.kl_constraint /
                              (torch.dot(descent_direction, Hd) + 1e-8))
        new_para = self.line_search(states, actions, advantage, old_log_probs,
                                    old_action_dists,
                                    descent_direction * max_coef)  # 线性搜索
        torch.nn.utils.convert_parameters.vector_to_parameters(
            new_para, self.actor.parameters())  # 用线性搜索后的参数更新策略

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'],
                              dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
            self.device)
        rewards = torch.tensor(transition_dict['rewards'],
                               dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'],
                                   dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'],
                             dtype=torch.float).view(-1, 1).to(self.device)
        td_target = rewards + self.gamma * self.critic(next_states) * (1 -
                                                                       dones)
        td_delta = td_target - self.critic(states)
        advantage = compute_advantage(self.gamma, self.lmbda,
                                      td_delta.cpu()).to(self.device)
        old_log_probs = torch.log(self.actor(states).gather(1,
                                                            actions)).detach()
        old_action_dists = torch.distributions.Categorical(
            self.actor(states).detach())
        critic_loss = torch.mean(
            F.mse_loss(self.critic(states), td_target.detach()))
        self.critic_optimizer.zero_grad()
        critic_loss.backward()
        self.critic_optimizer.step()  # 更新价值函数
        # 更新策略函数
        self.policy_learn(states, actions, old_action_dists, old_log_probs,
                          advantage)

PPO

而近端策略优化(Proximal Policy Optimization，简称 PPO)是A2C的一个变形，它是现在OpenAI默认的强化学习算法。

TRPO是通过约束使得KL散度不要太大，但是这个比较难算，PPO是在计算梯度的时候把约束融合进去，包含两个变种，其中最常用的是clip。

PPO-Penalty

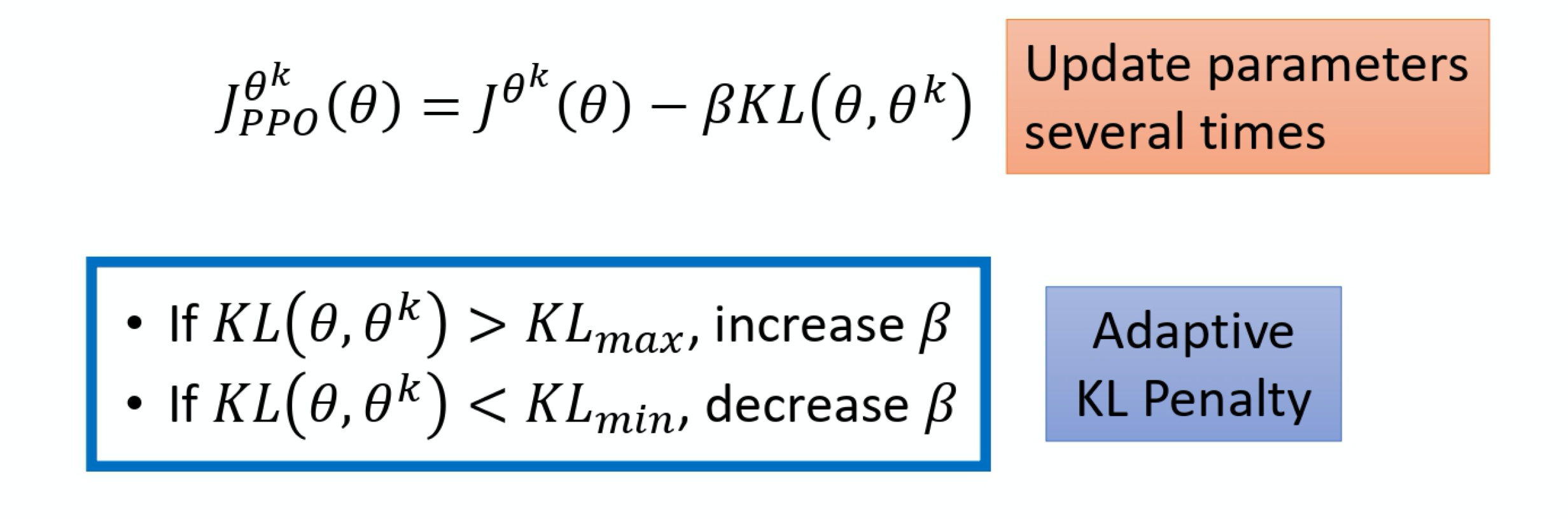通过自适应KL散度，让两个参数输出的动作差别减小

PPO-Clip

首先，定义旧策略（old policy）和新策略（new policy）的概率密度函数分别为 $\pi_{\theta_{old}}$ 和 $\pi_{\theta}$。
接着，定义似然比（likelihood ratio）：
$$r(\theta)=\frac{\pi_{\theta}(a|s)}{\pi_{\theta_{old}}(a|s)}$$

然后，定义 PPO 的目标函数：
$$\min_{\theta}\mathbb{E}\left[\min\left(r(\theta)\hat{A}_{t},clip(r(\theta),1-\epsilon,1+\epsilon)\hat{A}_t\right)\right]$$

其中，$\hat{A}_{t}$ 是优势函数估计，表示在状态 $s_t$ 选择动作 $a_t$ 的优势值。

在 PPO 中，还引入了一个超参数 $\epsilon$，称为 PPO 比例因子（PPO clipping factor），用于限制似然比的范围，避免更新过于剧烈。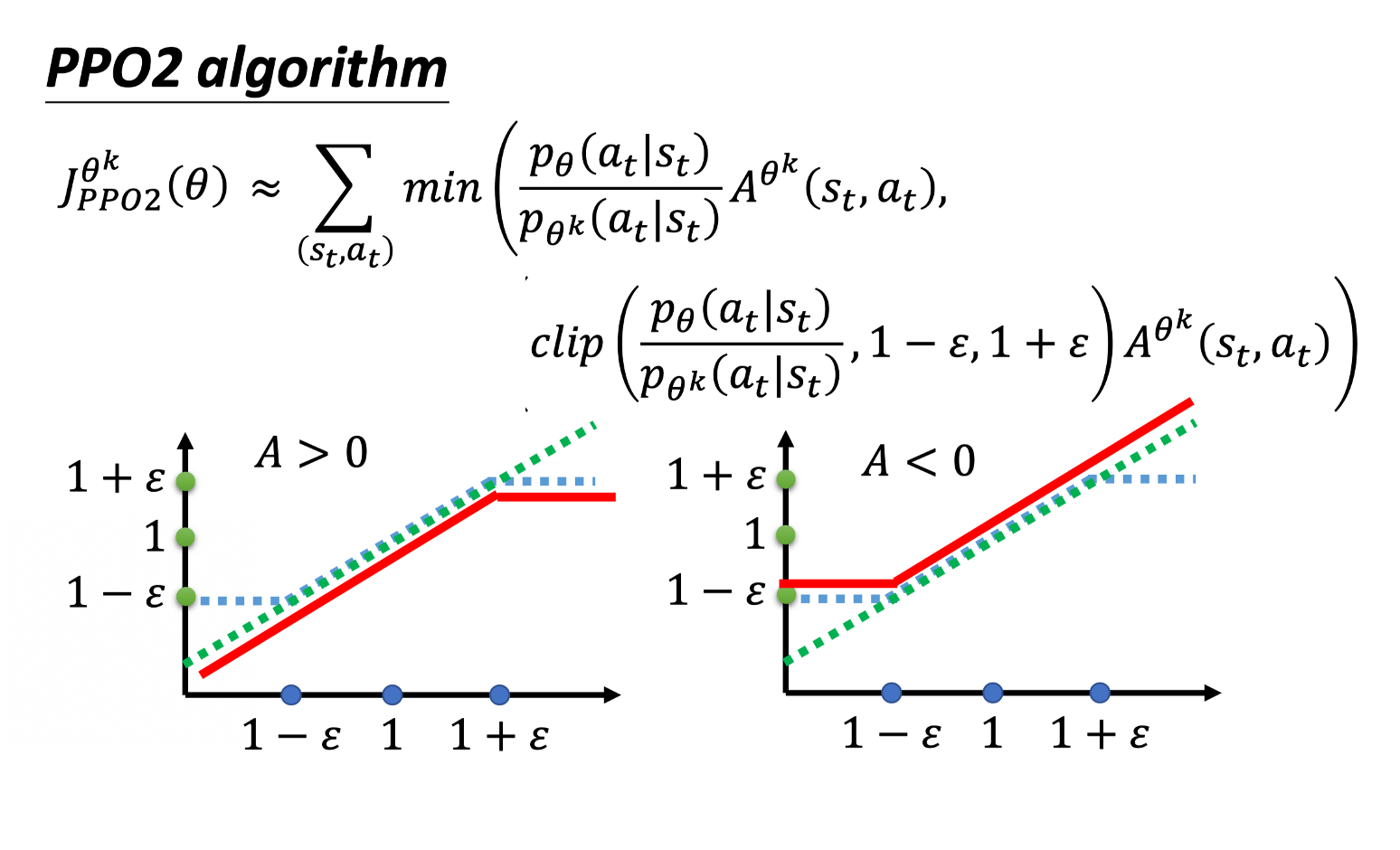

通过clip让参数的优化不要太过。

截断的效果比较好，而且非常简单；
通过观察梯度可以发现，截断就是限制重要性采样的比值，让新旧策略差别大的样本不起作用。

在实际中往往使用分布式强化学习，同时在多个环境采集数据，供模型训练，因此必然存在模型不同步的问题，而PPO可以较好的解决这个问题，因此PPO的应用非常广泛。

class PPO:
    ''' PPO算法,采用截断方式 '''
    def __init__(self, state_dim, hidden_dim, action_dim, actor_lr, critic_lr,
                 lmbda, epochs, eps, gamma, device):
        self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
        self.critic = ValueNet(state_dim, hidden_dim).to(device)
        self.actor_optimizer = torch.optim.Adam(self.actor.parameters(),
                                                lr=actor_lr)
        self.critic_optimizer = torch.optim.Adam(self.critic.parameters(),
                                                 lr=critic_lr)
        self.gamma = gamma
        self.lmbda = lmbda
        self.epochs = epochs  # 一条序列的数据用来训练轮数
        self.eps = eps  # PPO中截断范围的参数
        self.device = device

    def take_action(self, state):
        state = torch.tensor([state], dtype=torch.float).to(self.device)
        probs = self.actor(state)
        action_dist = torch.distributions.Categorical(probs)
        action = action_dist.sample()
        return action.item()

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'],
                              dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
            self.device)
        rewards = torch.tensor(transition_dict['rewards'],
                               dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'],
                                   dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'],
                             dtype=torch.float).view(-1, 1).to(self.device)
        td_target = rewards + self.gamma * self.critic(next_states) * (1 -
                                                                       dones)
        td_delta = td_target - self.critic(states)
        advantage = rl_utils.compute_advantage(self.gamma, self.lmbda,
                                               td_delta.cpu()).to(self.device)
        old_log_probs = torch.log(self.actor(states).gather(1,
                                                            actions)).detach()

        for _ in range(self.epochs):
            log_probs = torch.log(self.actor(states).gather(1, actions))
            ratio = torch.exp(log_probs - old_log_probs)
            surr1 = ratio * advantage
            surr2 = torch.clamp(ratio, 1 - self.eps,
                                1 + self.eps) * advantage  # 截断
            actor_loss = torch.mean(-torch.min(surr1, surr2))  # PPO损失函数
            critic_loss = torch.mean(
                F.mse_loss(self.critic(states), td_target.detach()))
            self.actor_optimizer.zero_grad()
            self.critic_optimizer.zero_grad()
            actor_loss.backward()
            critic_loss.backward()
            self.actor_optimizer.step()
            self.critic_optimizer.step()

其它技巧

此处参考The 37 Implementation Details of Proximal Policy Optimization，影响PPO算法性能的10个关键技巧

Advantage Normalization

优势函数的计算过程中，由于数据的不稳定性和样本方差的影响，导致训练过程不稳定，难以收敛到最优解。为了解决这个问题，Advantage Normalization技术被提出。

Advantage Normalization的基本思想是对采样的优势函数进行归一化处理，使得优势函数的期望值为0，方差为1。具体来说，先计算所有采样数据的优势函数的均值和标准差，然后对每个优势函数进行如下归一化处理：

$$\hat{A}(s_t,a_t)=\frac{A(s_t,a_t)-\mu}{\sigma}$$

其中，$\mu$和$\sigma$分别是所有采样数据的优势函数的均值和标准差，$A(s_t,a_t)$是当前状态下采取动作$a_t$的优势函数。

通过这种归一化处理，可以降低训练过程中采样数据的方差，提高训练的稳定性和收敛速度。在实际应用中，Advantage Normalization通常与其他技术如基准函数、策略梯度裁剪等一起使用，以进一步提高算法的性能和稳定性。

在使用GAE计算完一个batch的优势值后，对优势值进行减均值除标准差的Normalization；
可以在整个batch上做，也可以在minibatch上做，一般前者更好，因为后者波动更大。

State Normalization

对输入的状态值做减均值除标准差的Normalization；
因为强化学习的数据并非一开始就获得全部，因此不能像监督学习一样在数据预处理阶段统一进行；
可以动态维护所有获得过的state的mean和std，然后再对当前的state做normalization。

Reward Normalization & Reward Scaling

Reward Normalization：

• state normalization的操作类似，也是动态维护所有获得过的reward的mean和std，然后再对当前的reward做normalization

Reward Scaling：

• 通过指数滑动平均的方式维护标准差，然后只对reward除标准差

一般Reward Scaling的效果要好于Reward Normalization，Reward Normalization可以会破坏reward的结构

Policy Entropy

用熵来衡量策略给各个动作预测的概率值：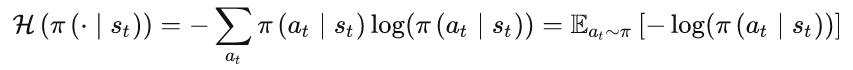

熵越大，说明策略给各个动作的预测更加平均，探索性更强，更有利于找到更优解
可以将熵加到loss上

Learning Rate Decay

通过学习率衰减，提升训练后期的平稳性

Gradient clip

加入Gradient clip防止训练的时候出现梯度爆炸

self.optimizer.zero_grad()
loss.mean().backward()
if self.use_grad_clip: 
    torch.nn.utils.clip_grad_norm_(self.parameters(), 0.5) 
self.optimizer.step()

Orthogonal Initialization

正交初始化（Orthogonal Initialization）是为了防止训练开始出现梯度消失和梯度爆炸的问题

• 用均值为0，标准差为1的高斯分布初始化权重矩阵；
• 对这个权重矩阵进行奇异值分解，得到两个正交矩阵，取其中之一作为该层神经网络的权重矩阵。

Adam Optimizer Epsilon Parameter

将pytorch中Adam优化器默认的eps=1e-8改为eps=1e-5，可以提升训练性能

Tanh Activation Function

把PPO的激活函数从relu改为tanh

done信号区分

环境结束除了输赢外还有达到最大步长的情况；
在计算目标时，输赢的结束只考虑奖励，而达到最大步长的结束还应该考虑下一个状态的值。

if done and episode_steps != args.max_episode_steps:
    dw = True
else:
    dw = False
...
deltas = r + self.gamma * (1.0 - dw) * vs_ - vs

动作空间分布

将连续动作空间的分布从Gaussian分布改为Beta分布。
因为前者是无界分布，还需要clip的操作，这会带来不好的影响

深度确定性策略梯度（DDPG）

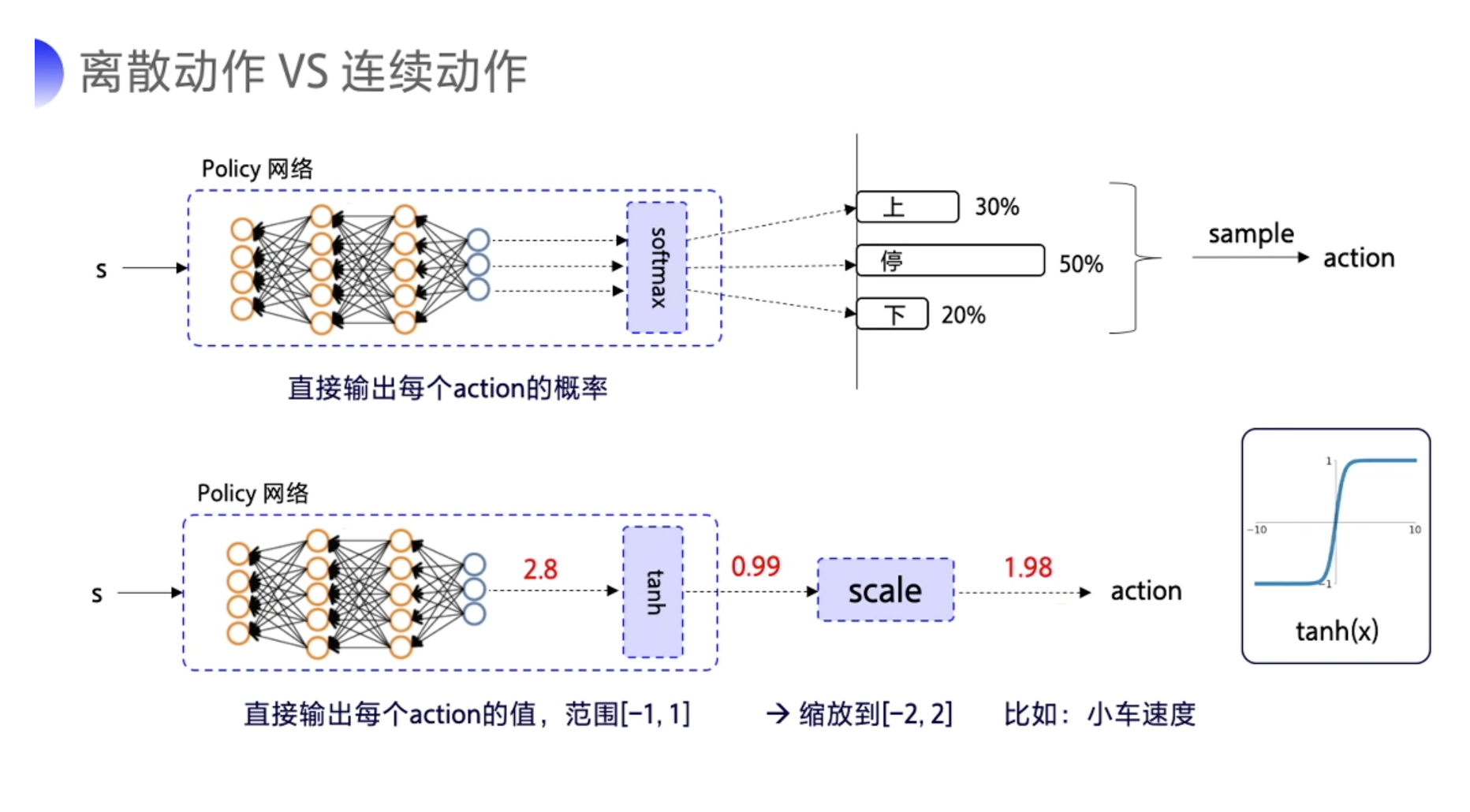
在连续的动作控制空间，Q-learning、DQN 等算法是没有办法处理的。这个时候可以使用策略网络。

• 在离散动作的场景下，有几个动作，神经网络就输出几个概率值，我们用$\pi_\theta(a_t|s_t)$来表示这个随机性的策略。
• 在连续的动作场景下，比如机器人手臂弯曲的角度，可以输出一个具体的浮点数。我们用$\mu_{\theta}(s_t)$来代表这个确定性的策略。

DDPG的特点可以从它的名字当中拆解出来，拆解成：

• Deep：深度网络
• Deterministic：输出确定的动作
• Policy Gradient：策略网络

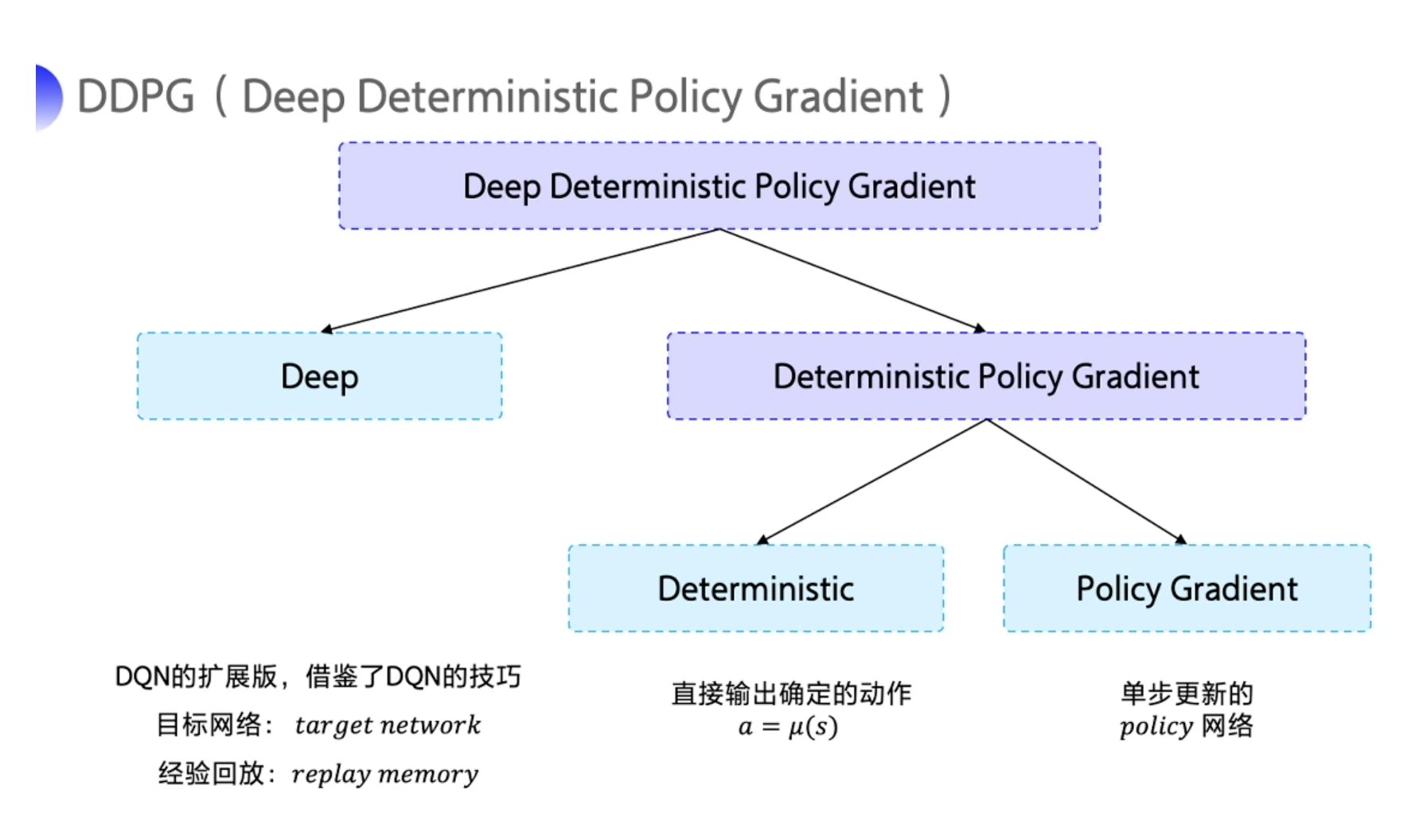
同时借鉴了DQN的目标网络和经验回放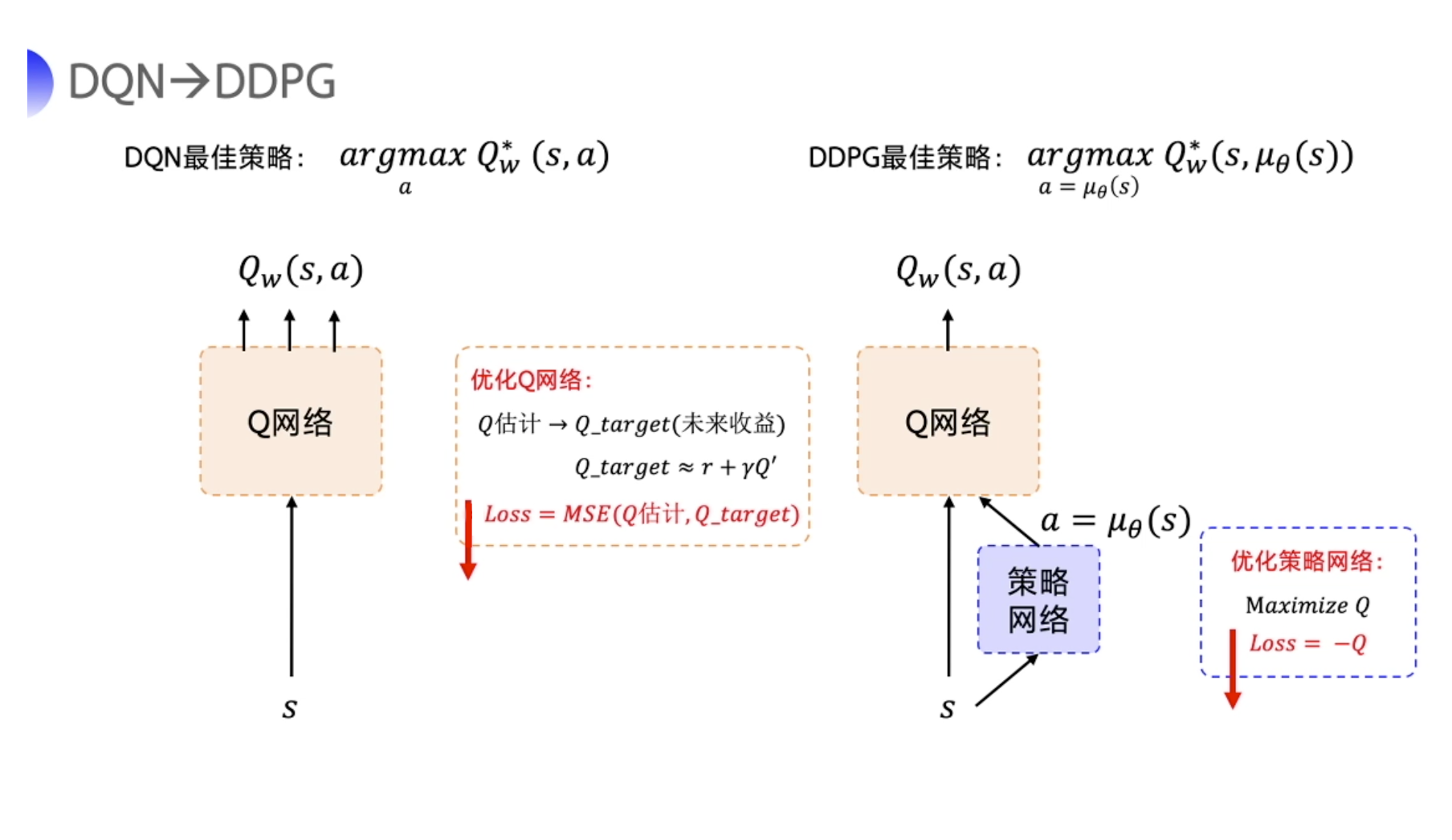

也属于AC网络。
Q网络和策略网络都有target network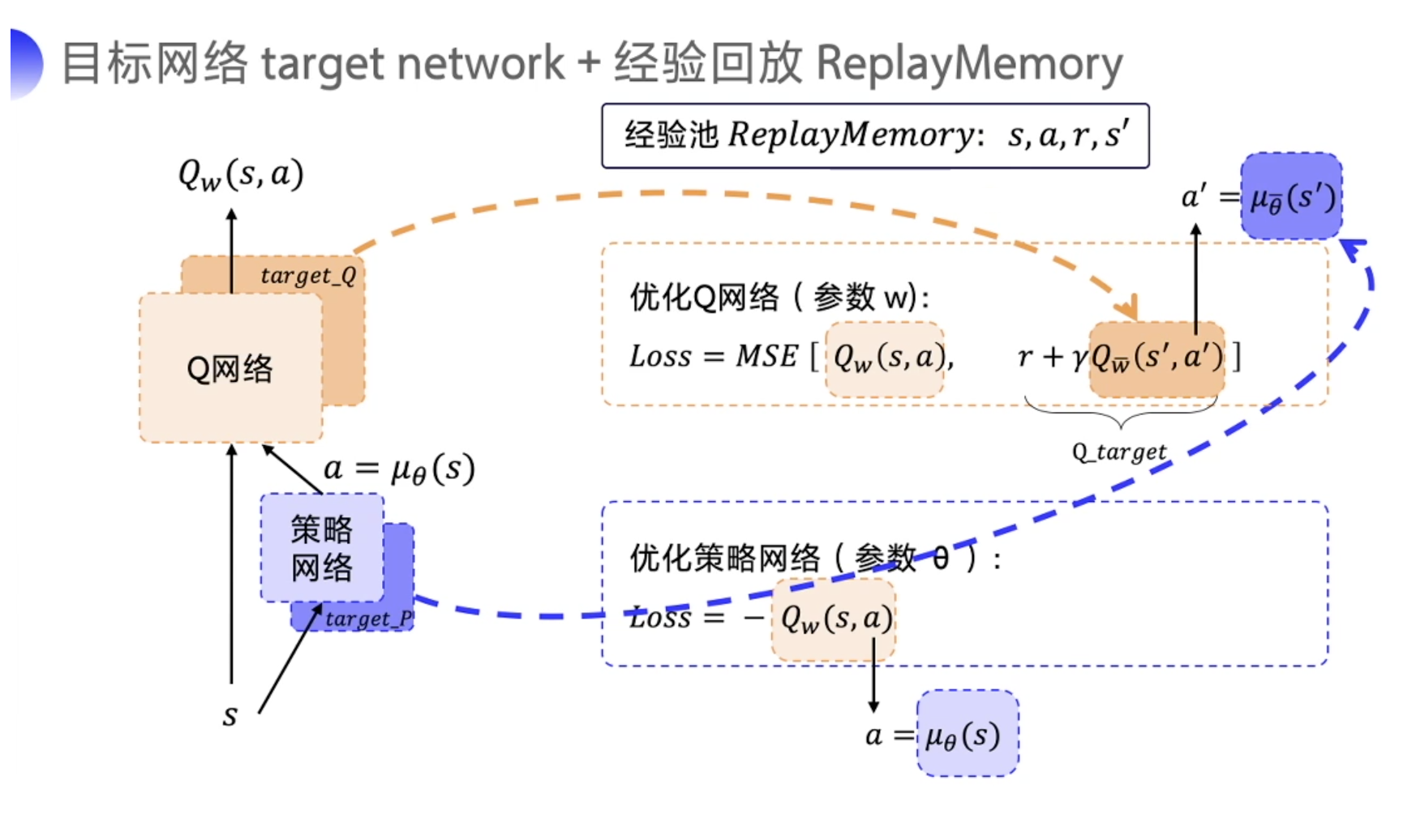

因为DDPG是使用的确定性策略，因此可能不会尝试足够多的action来找有用的学习信号；
可以通过加入时间相关的OU噪声或者高斯噪声来提高探索性。

class PolicyNet(torch.nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim, action_bound):
        super(PolicyNet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
        self.action_bound = action_bound  # action_bound是环境可以接受的动作最大值

    def forward(self, x):
        x = F.relu(self.fc1(x))
        return torch.tanh(self.fc2(x)) * self.action_bound


class QValueNet(torch.nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(QValueNet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim + action_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, hidden_dim)
        self.fc_out = torch.nn.Linear(hidden_dim, 1)

    def forward(self, x, a):
        cat = torch.cat([x, a], dim=1) # 拼接状态和动作
        x = F.relu(self.fc1(cat))
        x = F.relu(self.fc2(x))
        return self.fc_out(x)

class DDPG:
    ''' DDPG算法 '''
    def __init__(self, state_dim, hidden_dim, action_dim, action_bound, sigma, actor_lr, critic_lr, tau, gamma, device):
        self.actor = PolicyNet(state_dim, hidden_dim, action_dim, action_bound).to(device)
        self.critic = QValueNet(state_dim, hidden_dim, action_dim).to(device)
        self.target_actor = PolicyNet(state_dim, hidden_dim, action_dim, action_bound).to(device)
        self.target_critic = QValueNet(state_dim, hidden_dim, action_dim).to(device)
        # 初始化目标价值网络并设置和价值网络相同的参数
        self.target_critic.load_state_dict(self.critic.state_dict())
        # 初始化目标策略网络并设置和策略相同的参数
        self.target_actor.load_state_dict(self.actor.state_dict())
        self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
        self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)
        self.gamma = gamma
        self.sigma = sigma  # 高斯噪声的标准差,均值直接设为0
        self.tau = tau  # 目标网络软更新参数
        self.action_dim = action_dim
        self.device = device

    def take_action(self, state):
        state = torch.tensor([state], dtype=torch.float).to(self.device)
        action = self.actor(state).item()
        # 给动作添加噪声，增加探索
        action = action + self.sigma * np.random.randn(self.action_dim)
        return action

    def soft_update(self, net, target_net):
        for param_target, param in zip(target_net.parameters(), net.parameters()):
            param_target.data.copy_(param_target.data * (1.0 - self.tau) + param.data * self.tau)

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions'], dtype=torch.float).view(-1, 1).to(self.device)
        rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)

        next_q_values = self.target_critic(next_states, self.target_actor(next_states))
        q_targets = rewards + self.gamma * next_q_values * (1 - dones)
        critic_loss = torch.mean(F.mse_loss(self.critic(states, actions), q_targets))
        self.critic_optimizer.zero_grad()
        critic_loss.backward()
        self.critic_optimizer.step()

        actor_loss = -torch.mean(self.critic(states, self.actor(states)))
        self.actor_optimizer.zero_grad()
        actor_loss.backward()
        self.actor_optimizer.step()

        self.soft_update(self.actor, self.target_actor)  # 软更新策略网络
        self.soft_update(self.critic, self.target_critic)  # 软更新价值网络

Twin Delayed DDPG

DDPG有时表现很好，但它在超参数和其他类型的调整方面经常很敏感，双延迟深度确定性策略梯度(Twin Delayed DDPG，简称 TD3)引入三个关键技巧来解决

截断的双 Q 学习：同时训练两个Q函数，并使用Q值较小的来作为Q目标
$$ y\left(r, s^{\prime}, d\right)=r+\gamma(1-d) \min_{i=1,2} Q_{\phi_{i, t a r g}}\left(s^{\prime}, a_{T D 3}\left(s^{\prime}\right)\right) $$
延迟的策略更新：降低策略网络的更新频率
目标策略平滑：在目标动作中加入噪声，以平滑误差
$$ a_{T D 3}\left(s^{\prime}\right)=\operatorname{clip}\left(\mu_{\theta, t a r g}\left(s^{\prime}\right)+\operatorname{clip}(\epsilon,-c, c), a_{\text {low }}, a_{\text {high }}\right) $$

soft Actor Critic

SAC（Soft Actor-Critic）算法是一种用于连续动作空间下强化学习的算法，它是基于策略梯度算法和Q-learning算法的混合算法。SAC算法的主要目标是最大化奖励函数，同时最小化策略的熵，从而鼓励策略探索更多的动作，以提高探索效率和策略的稳定性。
SAC算法的关键点如下：

• 策略梯度算法：SAC算法使用了策略梯度算法来更新策略。具体来说，它使用一个近似策略梯度方法，即使用基于Q函数的渐进策略优化（ASO）来更新策略。
• Q-learning算法：SAC算法还使用了Q-learning算法来学习值函数。具体来说，它使用了一个双Q网络结构，用于估计状态-动作值函数，并使用贝尔曼方程来更新Q网络参数。
• 策略熵：SAC算法还引入了策略熵的概念。策略熵是指策略函数对动作的分布的熵，衡量策略的不确定性和探索程度。SAC算法的目标是最大化奖励函数同时最小化策略熵，以鼓励策略探索更多的动作，提高探索效率和策略的稳定性。
• 目标熵：为了平衡策略探索和利用，SAC算法使用一个目标熵来控制策略熵的大小。目标熵是一个固定的值，它可以调整探索程度。
• 自适应温度：SAC算法还使用了一个自适应温度参数来平衡策略熵和目标熵，以实现更好的探索和利用平衡。自适应温度参数通过在线更新得到，以最大化策略的期望回报。

总的来说，SAC算法是一种有效的强化学习算法，它通过综合使用策略梯度算法、Q-learning算法、策略熵和目标熵等方法，实现了对连续动作空间下的探索和利用平衡。它在许多连续动作空间下的强化学习任务中表现出了很好的效果。

基于模型

基于模型的强化学习算法由于具有一个环境模型，智能体可以额外和环境模型进行交互，对真实环境中样本的需求量往往就会减少，因此通常会比无模型的强化学习算法具有更低的样本复杂度。
但是环境模型可能并不准确，不能完全代替真实环境，因此基于模型的强化学习算法收敛后其策略的期望回报可能不如无模型的强化学习算法。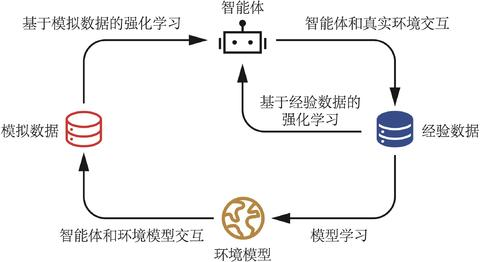

Dyna-Q

在Q-learning的基础上，将历史样本数据保存下来，每进行一次Q-learning更新后会进行n次Q-planning。
Q-planning会通过历史数据来更新。

模型预测控制

模型预测控制（MPC）包含两个迭代：

• 根据历史数据学习环境模型$P(s,a)$；
• 运用模型来选择动作。

打靶：生成候选序列的过程。
目的：生成多个序列，找到一个序列，使得序列的累计奖励最大。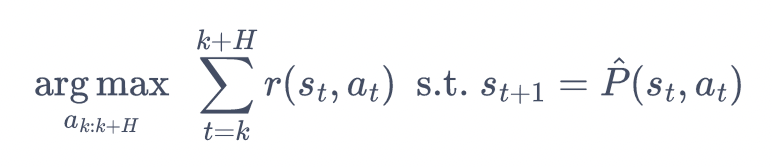

区别：推演多步，而非一步。

随机打靶法

生成多个序列时，动作是从动作空间中随机选取的
适用于简单环境

交叉熵法

交叉熵方法（cross entropy method，CEM）是一种进化策略方法：在一个带参数的分布中采样动作，并用选择的最优动作序列来更新分布

PETS

带有轨迹采样的概率集成（probabilistic ensembles with trajectory sampling，PETS）：采用集成学习的思想，生成多个环境模型，最后使用CEM预测动作，每个序列的每次动作都是用不同的模型来预测。
每个子模型输入状态动作对，输出下一个状态的分布：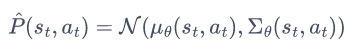

损失函数为：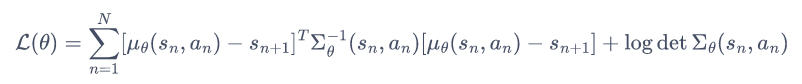

基于模型的策略优化

PETS等算法可以构建环境模型用于推演
Dyna算法可以通过历史数据来优化策略，减少交互数据的需求
因此基于模型的策略优化(MBPO)结合两者可以使用环境模型来生成数据，减少交互数据的需求

具体的，MBPO算法会把真实环境样本作为分支推演的起点，使用模型进行一定步数的推演，并用推演得到的模型数据用来训练模型。

在复杂环境中，MBPO的表现远远好于PETS算法

当模型误差、策略偏移程度较小时，可以采用较大的分支推演步数；反之要采用较小的分支推演步数，甚至不适合采用分支推演。

多智能体

博弈论

博弈论中的元素包括：

1. 玩家：在一个博弈中，玩家可以表示为 $i\in{1,2,…,n}$，其中 $n$ 表示博弈中玩家的数量。
2. 博弈形式：博弈形式可以表示为 $G=\langle N,(S_i),(u_i)\rangle$，其中 $N$ 表示玩家的集合，$(S_i)$ 表示每个玩家 $i$ 可以选择的策略集合，$u_i:S_1\times S_2\times…\times S_n\rightarrow\mathbb{R}$ 表示每个玩家在每个策略组合下的收益。
3. 策略：每个玩家 $i$ 可以执行的策略集合可以表示为 $S_i={s_{i1},s_{i2},…,s_{ik}}$，其中 $k$ 表示策略数量，$s_{ij}$ 表示第 $i$ 个玩家的第 $j$ 种策略。
4. 支付：每个玩家 $i$ 在执行策略组合 $(s_1,s_2,…,s_n)$ 后得到的支付可以表示为 $u_i(s_1,s_2,…,s_n)$。如果 $(s_1,s_2,…,s_n)$ 是 Nash均衡，那么 $u_i(s_1,s_2,…,s_n)$ 记为 $u^*_i$。
5. 理性和最优反应：通过比较不同策略组合下的支付，每个玩家都会选择最优策略。理性条件可以表示为 $u_i(s_1,s_2,…,s_i,…,s_n)\ge u_i(s_1,s_2,…,s’_i,…,s_n)$，即每个玩家 $i$ 会选择使自己获得最大收益的策略 $s_i$，而非其他的策略 $s’_i$。
6. Nash均衡：它表示在博弈中，每个玩家都采取了最佳策略，并且没有人可以单独改变其策略而获得更高的收益。如果策略组合 $(s_1,s_2,…,s_n)$ 满足每个玩家的策略都是最优的，那么该组合就是 Nash均衡，可以用 $(s^*_1,s^*_2,…,s^*_n)$ 表示。
7. 最小化和最大化：博弈论中常常有最小化和最大化的问题。最小化可以用 $\min$ 表示，最大化可以用 $\max$ 表示，例如 $\min_{s_i\in S_i}u_i(s_1,s_2,…,s_n)$ 和 $\max_{s_i\in S_i}u_i(s_1,s_2,…,s_n)$。

公共知识：
指的是所有参与博弈的玩家都知道的信息，这些信息通常是博弈中的基本参数，例如游戏的规则、策略、利润分布等等。公共知识可以影响每个玩家的行动和决策，因为每个玩家都会考虑其他参与者知道的信息和可能的行动。
公共知识是博弈论中的重要概念之一，因为它决定了每个玩家在博弈中了解到的信息和可能的行动，以及最终可能达成的结果。理解公共知识可以帮助玩家制定更有效的策略，并在博弈中取得更好的结果。

博弈论的类型：

1. 零和博弈：也称为完全竞争博弈，是指两个或多个参与者在有限的资源限制下进行竞争。在这种博弈中，每个参与者的收益完全相反，即一个参与者的收益必定是另一个参与者的损失，并且参与者之间是完全对抗的关系。
   公式：V(A)=-V(B)
   其中V(A)表示A的收益，V(B)表示B的收益。
2. 非零和博弈：与零和博弈不同，非零和博弈中，每个参与者的收益可以是正的、负的或者零。参与者之间的关系并不完全对抗，而是有一定的合作和协作。非零和博弈通常包括合作和竞争两个因素。
   公式：V(A,B)
   其中V(A,B)表示A和B的收益，可能是正的、负的或者零。
3. 合作博弈：合作博弈是指参与者通过合作来实现共同的目标，而不是通过竞争来获得个人利益。在这种博弈中，参与者需要共同合作，制定策略来达成目标。
   公式：v(S)
   其中v(S)表示参加集合S中的参与者总收益。
4. 非合作博弈：非合作博弈是指参与者通过竞争来获得个人利益，而不是通过合作实现共同目标。在这种博弈中，参与者独立制定策略，并通过互动来实现目标。
   公式：u(x,y)
   其中u(x,y)表示x和y参与非合作博弈的利润或效用。

概念

困难

当环境中存在多个智能体时，存在许多困难：

• 每个智能体所面对的环境是非稳态的；
• 多个智能体的训练可能是多目标的
• 训练评估的复杂度增加

任务视角

完全合作、完全竞争、混合

范式

• 完全中心化：将多个智能体进行决策当作一个超级智能体在进行决策，即把所有智能体的状态聚合在一起当作一个全局的超级状态，把所有智能体的动作连起来作为一个联合动作。
  • 环境稳态，可以保证收敛性
  • 不能应对智能体数量很多或者环境很大的情况
• 完全去中心化：每个智能体单独学习，不考虑其它智能体
  • 环境不稳态
  • 有利于扩展
• 中心化训练去中心化执行(CTDE)：训练的时候采用中心化，智能体可以得到一些全局信息，而执行时采用去中心化，得不到全局信息

去中心化

IPPO

独立 PPO（Independent PPO，IPPO）：每个智能体使用一个PPO算法单独训练
当智能体之间不需要合作，相互之间影响不大时比较合适。
当不同的智能体完全同质时，可以对不同智能体进行参数共享

基于AC的CTDE

中心化的值函数使用全局信息进行建模，较少考虑个体的特点；
在大规模较多个体时，值函数难以收敛和获得理想的策略；
同时仅依靠局部观测值，无法判断当前奖励是由于自身的行为还是环境中其他队友的行为而获得的。

MAPPO

在IPPO的基础上，将评论家进行中心化，让评论家可以观察到全局信息。
当然，如果智能体区别较大时，也可以使用不同的网络，不一定要参数共享，主要是要能看到全局信息。

MADDPG

采用DDPG算法，每个智能体的actor只能观察到局部信息，critic可以观察到全局信息
MADDPG针对连续动作，学习的是确定性策略。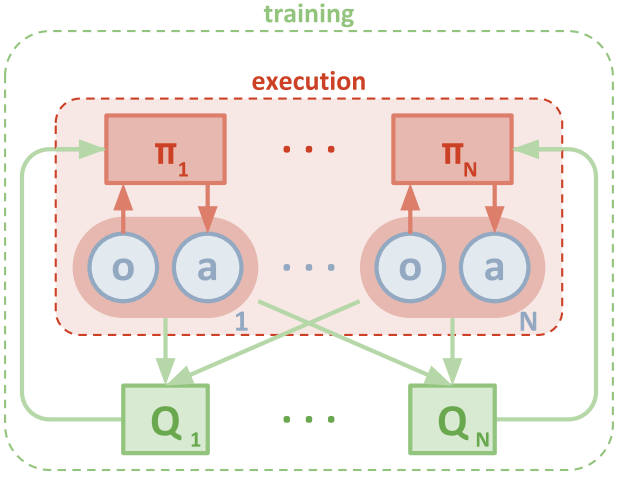

COMA

采用中心化训练、去中心化执行：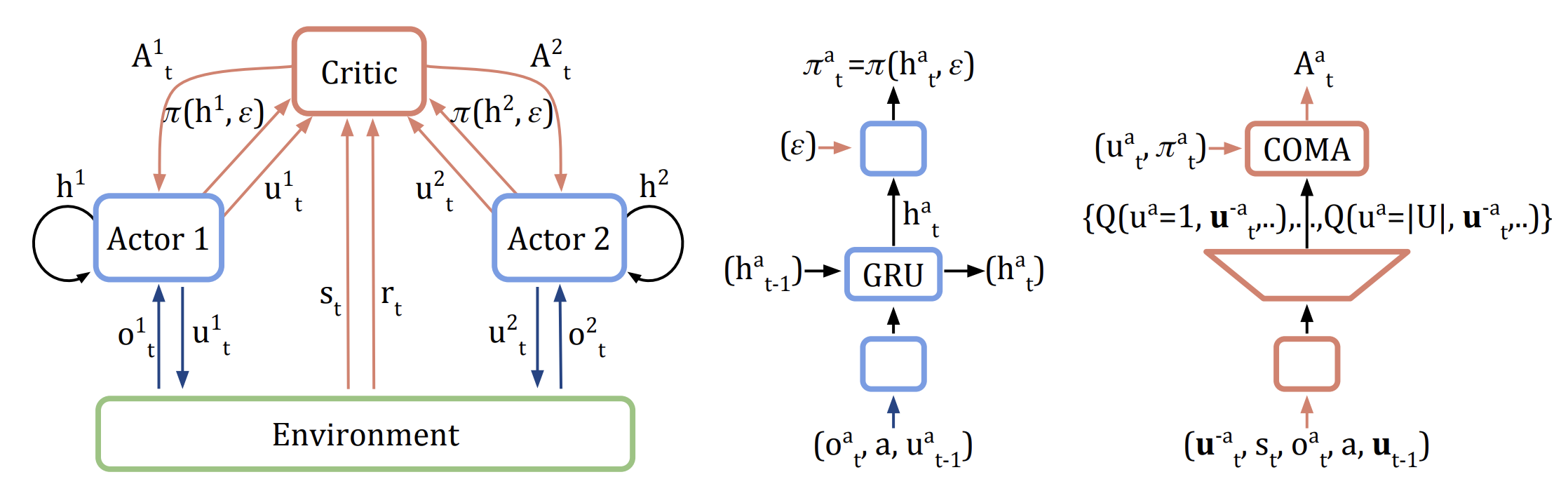

采用反事实基线（counterfactual baseline）来解决信用分配的问题
反事实基线（counterfactual baseline）即当前策略的平均效果：固定其它智能体的动作，计算当前动作相对默认动作的优势，计算优势函数。
COMA针对离散动作，学习的是​随机策略​。

基于value的CTDE

学一个总的value，并将这个value分配给各个智能体。

VDN

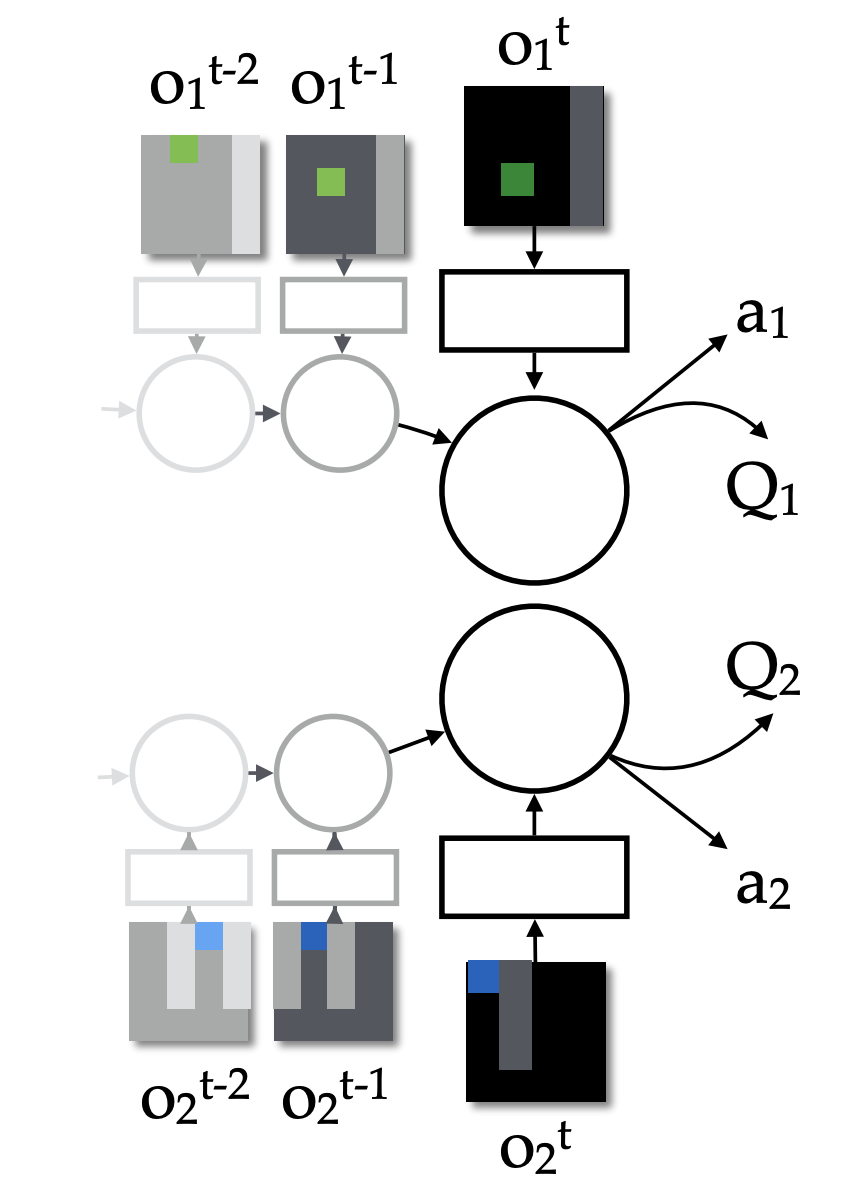如图，在多智能体场景下使用完全独立的agent，每个agent无法知道全局信息，只能最大化自己的收益，这样无法得到整体的最优解，可能存在囚徒困境等问题。 VDN在此基础上将各个智能体的Q值相加得到整体的Q值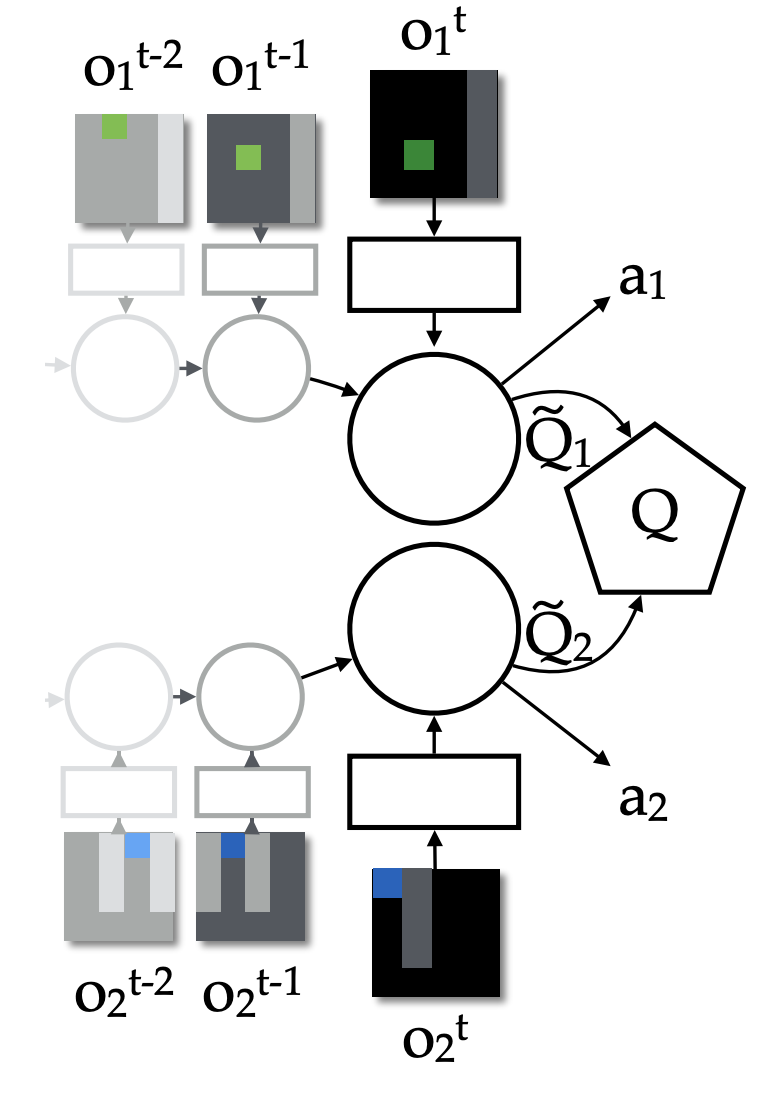： 各个agent可以根据情况进行参数共享或不共享。 通过优化整体的Q值来训练模型，而智能体选择动作时则依据自身的Q值。

QMIX

在VDN的基础上优化了整体Q值的计算：

• 通过神经网络计算而不是简单的相加；
• 另一方面引入了全局信息。

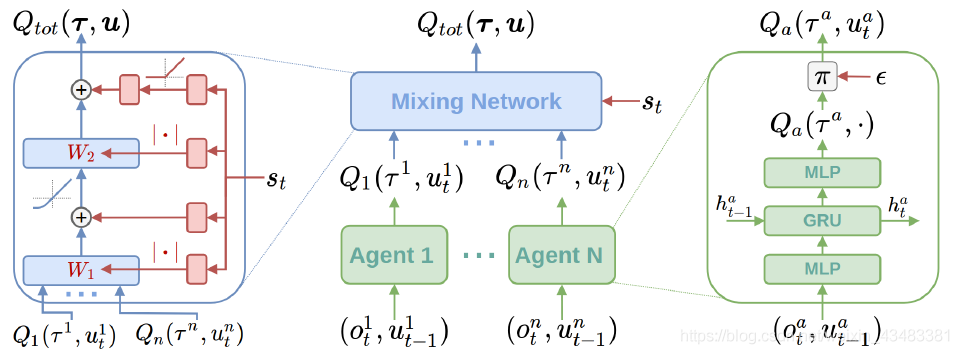
• 每个智能体都拥有一个DRQN网络（绿色块）：

  • 以个体的观测值作为输入；
  • 使用循环神经网络来保留和利用历史信息；
  • 输出个体的局部$Q_i$值。

• 局部$Q_i$值输入混合网络模块（蓝色块）:

  • 各层的权值是利用一个超网络（hypernetwork）以及绝对值计算产生的；
  • 利用全局状态s经过超网络来产生权值，能够更加充分和灵活地利用全局信息来估计联合动作的$Q$值，有助于全局$Q$值的学习和收敛；
  • 绝对值计算保证了权值是非负的、使得局部$Q_i$值的整合满足单调性约束；

• 最终的模型才用类似DQN的方式优化最终的$Q$：

  

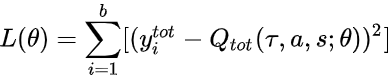
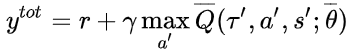
• 各个智能体采取动作只需要各自的$Q_i$值。

QTRAN

VDN和QMIX都保证了值分解的单调性，但单调性的约束是充分不必要的操作；
QTRAN将约束扩大为：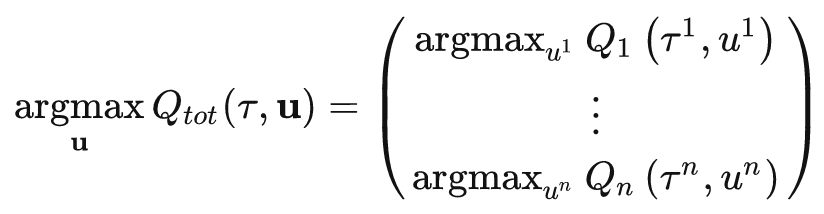

进而有机会得到更好的分解效果。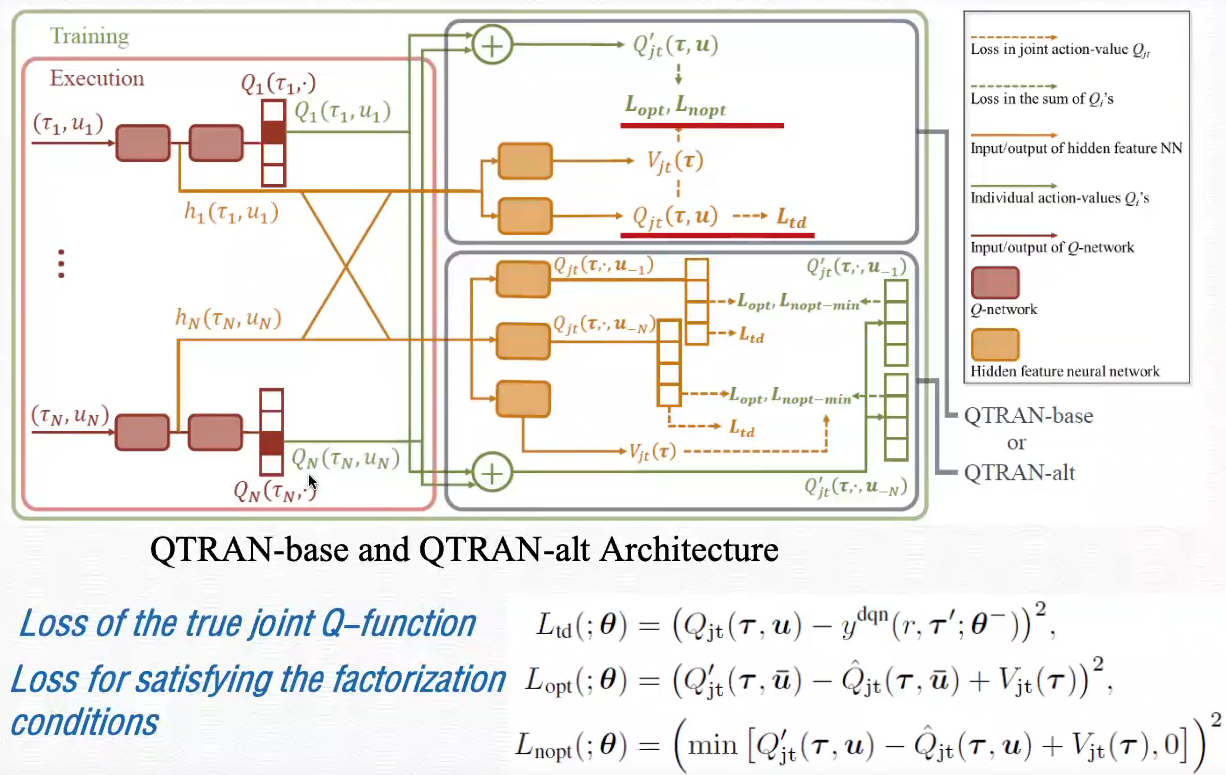

MAVEN

QMIX的问题：

• QMIX是一种满足单调性约束的Q值拟合器；
• 能够解决大部分MARL问题，但是对于非单调性的任务，QMIX的函数拟合能力就会受到比较大的限制；
• 这种限制也体现在智能体在联合动作空间中的探索上，由于智能体的策略总是满足单调性约束，因此探索也就被限制在一个特定的流形上，而不是整个联合动作空间。最后，算法就只能找到局部最优解。

MAVEN在QMIX的基础上增加了一个隐变量；
通过隐变量增加算法的探索性；
相当于同时学了很多Q值，就更容易跳出局部解。

Weighted QMIX

通过权重函数对每个联合动作的加权，映射到非单调值函数，并得到对应的最优策略，从而避免QMIX算法得到的策略陷入局部最优。

高级用法

稀疏奖励

很多场景下奖励和惩罚出现的频率很低，即稀疏，这样训练网络非常困难。

Reward Shaping

Reward shaping是强化学习中的一种技术，用于修改奖励信号，使其更符合问题的实际要求，从而加速学习过程并提高性能。通常来说，问题的奖励信号是非常稀疏的，即只有在任务完成时才会有非零奖励，这使得强化学习算法很难从奖励信号中学到有效的策略。因此，reward shaping的目标是通过添加附加的奖励信号来改进原始奖励信号。这样一来，智能体可以更好地理解任务的结构，更快地学习到合适的策略，并且可能能够在更短的时间内达到更好的性能。

例如，在一个机器人控制的任务中，如果只给机器人一个简单的“成功”或“失败”的二元奖励信号，很难让机器人从这个信号中学到什么有用的东西。但是，如果通过reward shaping添加了额外的奖励信号，例如在机器人朝着目标移动时距离目标的距离，或者在机器人走过特定的路径时给予奖励，智能体就可以更好地理解任务的要求，并学会更好的策略。

Curiosity

还可以设计一个好奇分数，将好奇分数加到价值上，增加智能体的探索：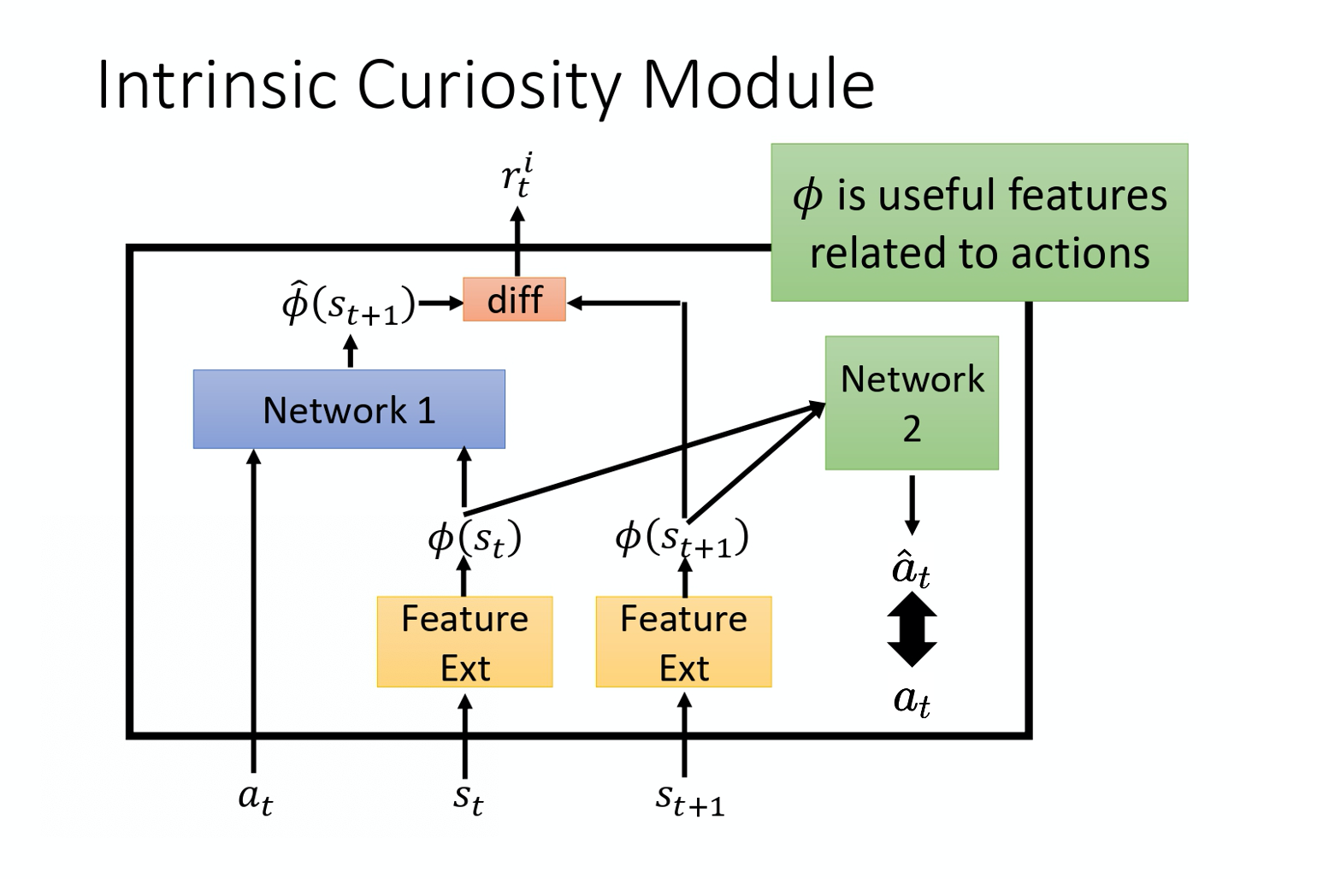

curriculum learning

让智能体从简单的场景、任务、数据学起，逐渐提高难度，这样可以更好地学习。

Curriculum learning是一种强化学习中的训练方法，它利用一些预先设定的学习任务序列，逐步提升智能体的学习难度和复杂度，让其能够逐渐适应复杂的环境和任务。Curriculum learning的核心思想是将学习任务按照难易程度进行分级，先让智能体学习容易的任务，逐渐增加任务难度，最终让其学会完成复杂的任务。通过这种逐步提高难度的方式，可以加快智能体的学习速度，提高训练效果。

Curriculum learning的应用领域非常广泛，可以用于解决各种问题，如图像识别、自然语言处理、机器翻译、游戏智能等。在强化学习中，Curriculum learning可以帮助智能体在学习过程中降低学习难度，从而避免因训练困难而导致的效果下降和训练时间过长等问题。

reverse curriculum learning可以控制智能体的初始状态，开始的时候离最终状态近，更加容易学习。

分层强化学习

将一个复杂的强化学习问题分解成多个小的、简单的子问题，每个子问题都可以单独用马尔可夫决策过程来建模。这样，我们可以将智能体的策略分为高层次策略和低层次策略，高层次策略根据当前状态决定如何执行低层次策略。这样，智能体就可以解决一些非常复杂的任务。
分层强化学习通常被用于解决复杂的任务，例如机器人控制、策略游戏等。它可以大大减少需要学习的策略数量，从而提高学习效率。

模仿学习

模仿学习（imitation learning，IL）讨论连奖励都没有的场景，或者不能直接在环境中学习的场景，又叫：示范学习（learning from demonstration），学徒学习（apprenticeship learning），观察学习（learning by watching）
如：聊天机器人、自动驾驶、推荐系统。

行为克隆

类似于监督学习，让机器根据数据学习人的行为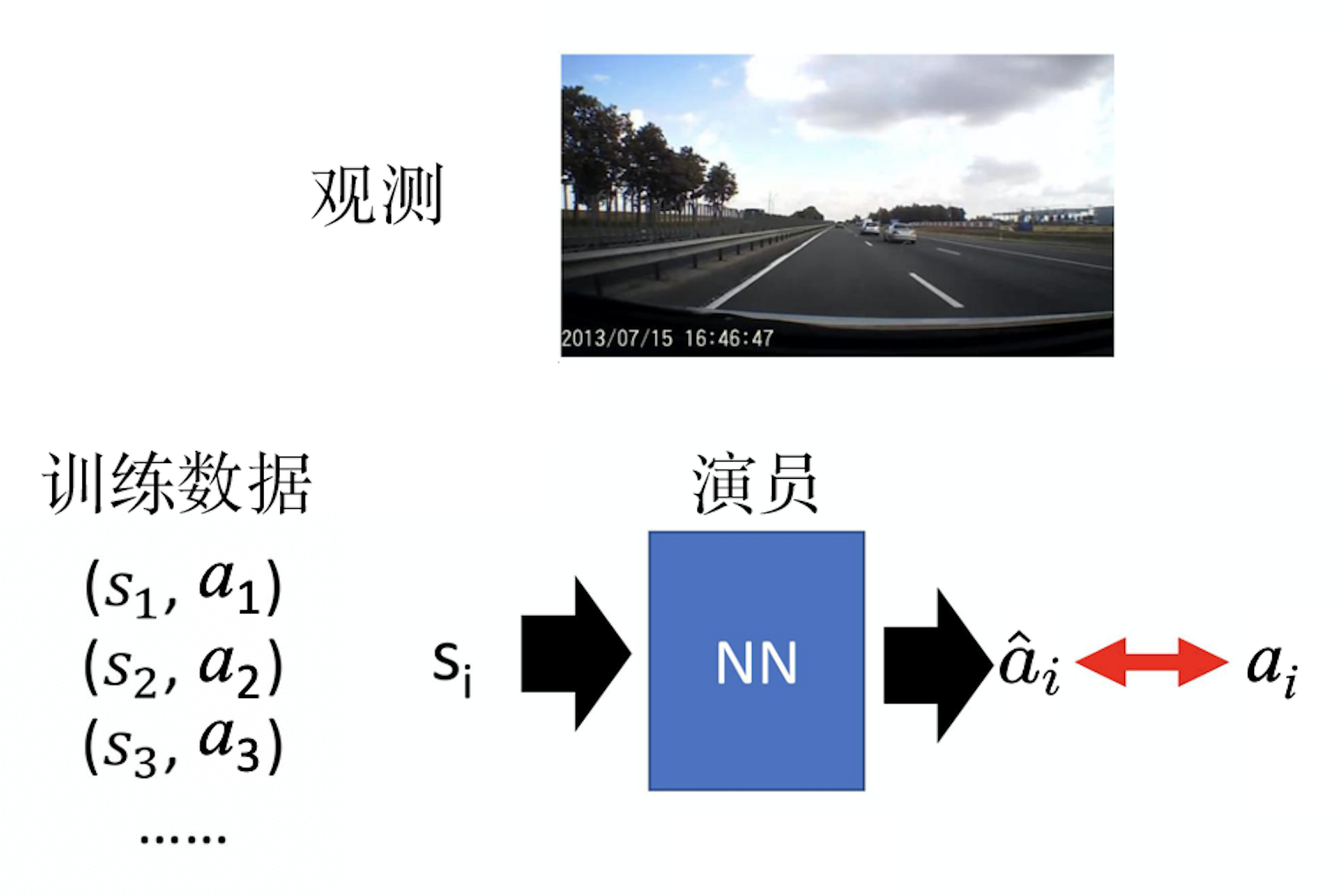

• 但是人的数据非常有限，很多情况覆盖不到，会出现分布偏移的情况
  • 智能体的决策和专家有区别，使得智能体发展到专家未覆盖到的场景
  • 可以通过数据融合：让人类来标注新的环境；较为困难
• 另外机器可能（过拟合）完全模范专家；
  • 学了一些没有必要的动作

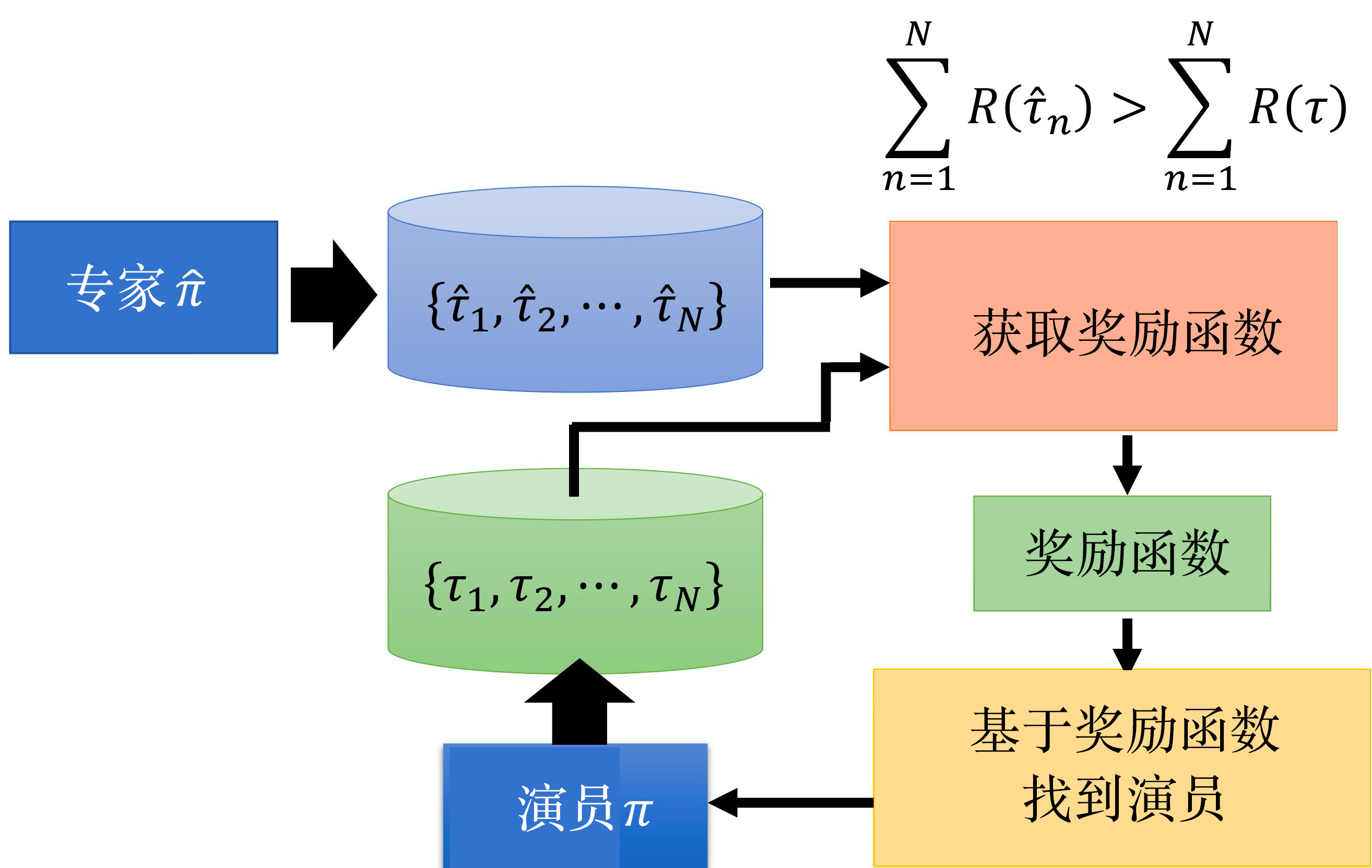
逆强化学习

1. 根据专家行为来学习奖励函数；
2. 根据奖励函数找到最优演员；
3. 调整奖励函数使得专家奖励优于演员；
4. 回到第二步继续优化演员，直到专家和演员的分数无法调整出差别即收敛。

与生成对抗网络的区别：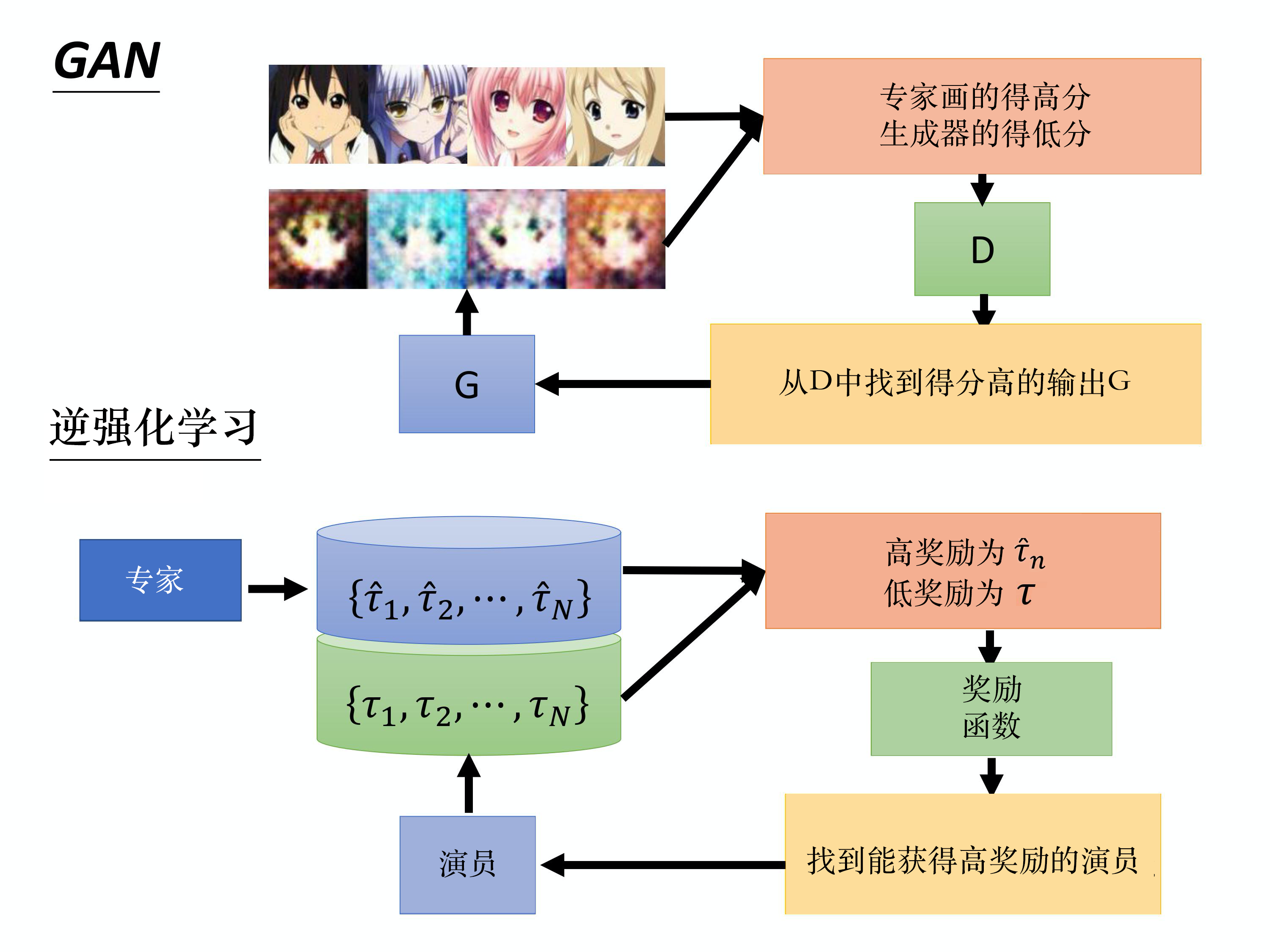

优势：往往不需要太多数据，因为只需要少数示范。

自博弈

naive self-paly

让智能体不断地和最新的模型对打，提升策略。
naive self-play可能出现剪刀石头布这样的循环学习，或者难以发现潜在的问题。

fictitious self-paly

让智能体不断地和所以历史模型对打，提升策略。

1. 智能体与随机策略对战；
2. 当智能体胜率超过一定阈值时，将智能体当前参数固化为一个历史策略；
3. 智能体与所有历史策略对战；
4. 跳回第2步，循环往复，不断提高。

class SelfPlayCallback(DefaultCallbacks):
    def __init__(self):
        super().__init__()
        # 0=RandomPolicy, 1=1st main policy snapshot,
        # 2=2nd main policy snapshot, etc..
        self.current_opponent = 0

    def on_train_result(self, *, algorithm, result, **kwargs):
        # Get the win rate for the train batch.
        # Note that normally, one should set up a proper evaluation config,
        # such that evaluation always happens on the already updated policy,
        # instead of on the already used train_batch.
        print(f"Iter={algorithm.iteration} win-rate={win_rate} -> ", end="")
        # If win rate is good -> Snapshot current policy and play against
        # it next, keeping the snapshot fixed and only improving the "main"
        # policy.
        if win_rate > args.win_rate_threshold:
            self.current_opponent += 1
            new_pol_id = f"main_v{self.current_opponent}"
            print(f"adding new opponent to the mix ({new_pol_id}).")
            # Re-define the mapping function, such that "main" is forced
            # to play against any of the previously played policies
            # (excluding "random").
            def policy_mapping_fn(agent_id, episode, worker, **kwargs):
                # agent_id = [0|1] -> policy depends on episode ID
                # This way, we make sure that both policies sometimes play
                # (start player) and sometimes agent1 (player to move 2nd).
                return (
                    "main"
                    if agent_id % 2 == 0
                    else "main_v{}".format(
                        np.random.choice(list(range(1,self.current_opponent + 1)))
                    )
                )

            new_policy = algorithm.add_policy(
                policy_id=new_pol_id,
                policy_cls=type(algorithm.get_policy("main")),
                policy_mapping_fn=policy_mapping_fn,
            )

            # Set the weights of the new policy to the main policy.
            # We'll keep training the main policy, whereas `new_pol_id` will
            # remain fixed.
            main_state = algorithm.get_policy("main").get_state()
            new_policy.set_state(main_state)
            # We need to sync the just copied local weights (from main policy)
            # to all the remote workers as well.
            algorithm.workers.sync_weights()
        else:
            print("not good enough; will keep learning ...")

        # +2 = main + random
        result["league_size"] = self.current_opponent + 2

heuristic fictitious self-paly

以一定的概率选择最新的或者历史的

rank-based fictitious self-paly

将对手策略分级，选择合适级别的策略来对打

policy-spaced response oracles

league base self-play

基于联盟的智能体分为3种：主智能体（main agent）、联盟利用者（league exploiter）和主利用者（main exploiter）：

• 主智能体：即主力选手，正在训练的智能体及其祖先。其有50%使用PFSP方法从联盟模型池中进行采样，使用有优先级的虚拟自学习策略，即能打败智能体的采样概率高，不能打败智能体的采样概率低。有35%概率使用传统Self-Play自对弈方式按照一定概率分布选择Main Agent历史模型，有15%从已经淘汰的历史对手中进行随机挑选（即Main Agent对战这些智能体胜率已经达到100%）。
• 主利用者：即主力选手的陪练，能打败训练中的所有智能体。在训练的过程中，随机从3个智能体中挑选1个主智能体，如果可以以高于0.1的概率打败该智能体就与其进行训练，如果不能就从之前的主智能体中再挑选对手。当以0.7的胜率打败全部3个正在学习的主智能体时，或者距上次存档4*10^9步之后就保存策略，并且进行重设初始化策略的操作。
• 联盟利用者：即所有选手的陪练，能打败联盟中的所有智能体。其按照有优先级的虚拟自学习策略计算的概率与全联盟的对手训练，在以0.7的胜率打败所有的智能体或者距离上次存档2*10^9步后就保存策略，并且在存档的时候，有0.25概率把场上的联盟利用者的策略重设成监督学习初始化的策略。

他们的区别在于：如何选取训练过程中对战的对手；在什么情况下存档（snapshot）现在的策略；以多大的概率将策略参数重设为监督学习给出的初始化参数。

离线强化学习

在智能体学习的早期，所做的决策还非常不好的时候，不适合将智能体的决策直接反馈到真实环境中，此时可以使用离线强化学习。
离线强化学习是一种强化学习的方法，它是指智能体利用先前的数据来进行学习，而不是在实时环境中进行学习。与在线强化学习不同，离线强化学习允许智能体在大量数据上进行学习，从而更有效地利用数据和资源。离线学习通常使用深度学习算法，如深度Q网络（DQN）和深度确定性策略梯度（DDPG），这些算法能够从离线数据中识别出有用的模式和规律。尽管离线学习的效率更高，但需要注意的是，因为离线学习依赖于先前的数据，因此数据需要是具有代表性的，以确保训练的模型能够在实时环境中表现良好。

在某些领域中，构建仿真环境是一种常见的方法，例如无人车驾驶、机器人控制等。通过构建仿真环境，我们可以收集大量的训练数据，并在安全的情况下对智能体进行训练和评估。实际上，在一些复杂场景下，提供足够的现实数据并不容易，因此使用仿真数据进行训练可以大大降低数据采集成本。
除了使用仿真环境外，离线强化学习还可以使用历史数据、模拟数据和合成数据等方式进行训练，这些数据可以从环境中获取，也可以从其他来源（例如已建立的数据库）中获取，用于训练强化学习模型。

外推误差

外推误差：是指由于当前策略可能访问到的状态动作对与从数据集中采样得到的状态动作对的分布不匹配而产生的误差。
外推误差在离线强化学习中非常明显，会直接导致优化失败。

批量限制策略

通过选择与最优可能的数据来减小外推误差

推荐系统

离线强化学习用于推荐系统时，一般是基于历史用户行为数据来训练一个用户模型，并将该用户模型用作强化学习的环境，在此基础上训练智能体。
具体而言，用户模型是一个将用户的历史行为转换为状态的函数，通常采用基于深度学习的方法进行训练，例如使用RNN或卷积神经网络来学习用户的序列行为。
在训练智能体时，需要将用户模型作为环境来进行训练。在离线学习中，我们可以根据用户模型的预测结果来计算奖励或评估智能体的性能。在每个时间步，智能体输出一个推荐项，用户模型预测用户的反馈，并根据反馈计算奖励。奖励信号被用来更新智能体的策略，从而提高推荐的效果。
总之，离线强化学习用于推荐系统时，传统的监督学习方法只能学习到用户行为的概率分布，但是离线强化学习不仅能够学习用户行为的概率分布，还能够学习到如何最大化用户互动的奖励。因此，离线强化学习在推荐系统中具有重要的应用价值。

目标导向的强化学习

• 当环境有小幅改变时，经典的算法需要重新训练
• 许多环境的奖励信号非常稀疏

目标导向的强化学习会在策略网络、值网络的输入加上一个目标，这样可以给经验库中的数据加上合适的目标使得奖励信号变得稠密；同时可以应对目标变动的情况。

HER

事后经验回放（hindsight experience replay，HER）是在数据层面应用目标导向的思想。

实验总结

算法思想

强化学习包含许多基本模块和思路，这些模块和思路分别被提出用以解决不同问题，当所面对的场景符合时，可以尝试拿来主义，将合适的思想进行有机的结合。

模块

• 值函数：相对容易优化，可以评估状态或者状态动作对的价值
• 策略网络：可以直接根据状态输出动作，可用于连续动作空间
• 模型：可以用于推演预测、或生成数据，以提升智能体的泛化性、采取更优解的概率
• 离线训练缓存：可以减少对交互数据的需求

思路

调参总结

奖励

• 奖励函数的设置非常重要：
  • 要设置合适的奖励，智能体才能找到学习方向；
  • 奖励的设置要平衡，不能过与密集；
  • 奖励过于稀疏的话智能体很难探索到；

环境

• 多线程&矢量化：
  • 提升数据采集效率
  • 注意多线程对训练批次等的影响
• 对环境做一些合理地包装，使得环境提供的状态信息量更充足，信息密度更大；奖励函数更加合适

状态空间

• 做合适的Normalize

训练

• 批次大小：
  • 小批次更大的随机性；
  • 大批次更稳定
  • 要注意不同场景下批次的含义，有的是时间步，有的是轮数
• 每个iter用相同样本做多少次SGD：num_sgd_iter
  • 数量更大可以更加充分使用样本；
  • 但是可能容易对这些样本过拟合；
  • 尤其是在self-play中可能胜率很高但没有学到东西。
• 目标网络更新周期：
  • 太长了会难以收敛，因为两个网络差别大
  • 太短了两个网络一样会直接躺平
• 学习率：当模型效果难以提升的时候，需要降低学习率，去学习更加精细的信息。

保存

• 及时保存较好的模型
• 将测试保存成视频

  import os, cv2
  def test_avi(model, env, video_folder: str) -> None:
      fps = 6
      img_size = (160,210)
      if not os.path.exists(video_folder):
          os.makedirs(video_folder)
      video_dir = video_folder +'/'+ str(int(time.time())) + '.avi'
      fourcc = cv2.VideoWriter_fourcc(*'MJPG') #opencv3.0
      videoWriter = cv2.VideoWriter(video_dir, fourcc, fps, img_size)
      obs = env.reset()
      score = 0
      while True:
          img_data = env.render(mode='rgb_array')
          videoWriter.write(img_data)
          action, _states = model.predict(obs, deterministic=True)
          obs, reward, done, info = env.step(action)
          score += reward
          if done:
            break
      print("score: ", score)
      env.close()